Create LAMBDA Functions in Excel
This article provides a guide for learning to write your own custom functions in Excel using LAMBDA. Before continuing, make sure that you have a basic understanding of the LAMBDA function in Excel, by reading this article:
Must Read First: The LAMBDA Function in Excel - at support.microsoft.com
Table of Contents
Other Prerequisites: It will definitely help to have a healthy understanding of the various dynamic array functions in Excel, especially SEQUENCE. It also helps to familiarize yourself with All Excel functions. You don't need to know how to use them all, but if you are at least aware that a function exists, you'll be able to learn about that tool when you need it. Also, consider using AI and asking "I need an Excel function for ...".
Start with the LET Function
=LET(name1, value1, [name2], [value2],..., return_value_or_calculation)
The LET function allows you to define variables once and then reuse those variables within the rest of your formula. You can have any number of name/value pairs, and then the final parameter is the calculation or value that you want to return.
In addition to improving efficiency, the LET function makes formulas easier to understand, especially very complex formulas. Writing a LAMBDA function is like coding, so it is good practice to use common naming conventions for variables, indenting, etc.
Compare This:
=5*A37:A250^3 + 3*A37:A250^2 + 5*B37:B250 - 2*A37:A250*B37:B250 + 25
To This:
=LET( x, A37:A250, y, B37:B250, 5*x^3 + 3*x^2 + 5*y - 2*x*y + 25 )
In this basic LET example, we've defined the name "x" to be the range A37:A250, then the name "y" to be the range B37:B250. Then the final parameter is our function that uses the names x and y.
With LET, you do not need to use the name manager to define x and y, because these names only exist within the scope of the containing LET function.
Developer Tip: For debugging, also name your final calculation so that you can easily change the final line from "result" to "x" or any other intermediate result to check the values.
=LET( x, A37:A250, y, B37:B250, result, 5*x^3 + 3*x^2 + 5*y - 2*x*y + 25, result )
Create Your First LAMBDA Function
=LAMBDA(param1, [param2], ..., [paramN], return_value_or_calculation)
Start with LET
To see how closely LET and LAMBDA are related, we will first create a formula for the area of a rectangle using the LET function. Define the variables named "length" and "width" and assign them values, then return the calculation:
=LET( length, B2, width, B3, length * width )
By the way, I learned this technique of first writing a LET function and then converting it to a LAMBDA from an expert, Diarmuid Early. It is especially helpful while debugging a complex formula.
Change to LAMBDA
Change LET to LAMBDA and move the references to the end.
Using the LAMBDA function within a cell without naming it requires that you specify the input parameters in a second set of parenthesis. Compare the following function to the above LET function, noting the locations of the red references.
=LAMBDA( length, width, length * width )(B2,B3)
It may seem strange that the references are included at the end, but it makes sense when you replace "LAMBDA(...)" with your new function name like =areaRectangle(B2,B3). If you are using LAMBDA within a helper function (like BYROW, BYCOL, MAP, etc) or naming it within LET, then you won't need to put the references at the end.
Name the Function
The final step is to create a Named Function using the LAMBDA function we just created. Copy the formula up to but not including the references in red.
Go to Formulas > Name Manager and click on New.
In the Refers To field, paste the LAMBDA function that you just copied.
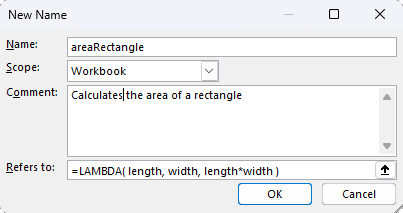
Here is the new formula that we can use anywhere in our workbook:
=areaRectangle( length, width)
If you start typing the name "area..." then Excel will pull up the name completion box which contains (1) defined named ranges (2) named functions and (3) built-in Excel functions. So, here is where we need to talk about naming conventions for your LAMBDA functions.
Naming Conventions for LAMBDA Functions
There are a lot of different ways to name functions, including ALLCAPS, CamelCase, lowerCamelCase, and all_lower_case. Another common method is to begin the function name with just an underscore like _FUNCTION.
The functions in the LAMBDA Library use ALLCAPS for 2 main reasons: (1) Built-in functions in Excel are all uppercase and (2) Named Functions in Google Sheets are forced to be uppercase.
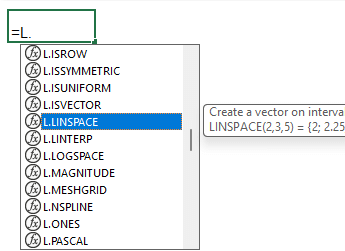
"L." Prefix - In our template file you will find that the functions all use the prefix "L.". This helps to distinguish the function names from built-in Excel functions. Also, as you type "=L." within a cell, Excel will show the entire list of custom functions that begin with L.
The "L." prefix is needed because the lambda functions were imported and saved into a module named "L" using the Excel Labs add-in. YOU can import functions into your own module. If you name the module "MY" then you would use the "MY." prefix before each function.
In Google Sheets, we are still using an "L_" prefix to differentiate the custom functions from the built-in spreadsheet functions.
Many of the functions in this library are similar to functions in Matlab and NumPy, so we have intentionally used function names that are similar to Matlab and NumPy to aid those who may be used to these other tools.
Naming Conventions for Parameter Names
Within your functions, you'll want to balance conciseness with descriptiveness when it comes to naming parameters, leaning more towards descriptiveness. Here are the conventions I have chosen to try to follow:
- Use descriptive nouns because intuitive code requires less commenting
- Always lowercase or lowerCamelCase
- Remember that LAMBDA parameter names will be shown in the function tooltip, so the name should be helpful
- Single-letter parameters are okay for indices and already-understood function behavior such as (acc,v) for (accumulator, current value)
- m,n are typically sizes (m for rows, n for columns)
- i,j,k are typically indices that may be incremented
- Anything that is a cell reference such as a1, v1, seq1 is invalid as a parameter name. Use underscores instead or spell it out: array_1, vector_1
Commenting within Named Functions
Althouth the Excel Labs Advanced Formula Editor (AFE) allows code commenting within function code (using // and /* */), comments are stripped out before the add-in creates the Named Function that shows up in the Name Manager.
There are two main ways to include comments that will persist as the Named Functions are used throughout other workbooks:
Method 1: Add a description via the Comment field in the Name Manager. This description will show up as a tooltip.
If using the Excel Labs AFE module, the description is added automatically using a special syntax for a comment immediately before the lambda definition, like this:
/**
* Function description within Comments field
* Note the two asterisks at the start "/**"
*/
FUNCTIONNAME =LAMBDA(...)
Method 2: Use LET within your LAMBDA function and add comments using named parameters like rem_1, rem_2, etc. The LAMBDA Library functions use this technique to define the url of the documentation page for each function.
=LAMBDA(param_1,param_2, LET(doc,"https://www.vertex42.com/lambda/", ...,..., rem_1,"A comment", ...,..., rem_2,"Another comment", ... ))
Define a Function with LET
There may be times when you not only want to name and reuse parameters with LET, but also create a named function. This is very simple, but the use cases can be very powerful.
The following example would be unnecessarily complex (for something as simple as squaring a value), but it shows that you can define a function within another function.
/** * Square a number, SQR(num) */ SQR =LAMBDA(num, LET( mySquare, LAMBDA(value, value^2), mySquare(num) ));
A working practical example is the ROT_90 function which rotates an array 90 degrees. This function could have been written to rely on the FLIP function. Instead, the ROT90 function uses LET to define its own version of the flip function.
It's usually better practice to only define a function one time. However, in many cases like FLIP, the function may be simple enough that you would rather redefine it than require that a function rely on other custom functions.
The EIGENVALUE function is an example of a complex formula that relies on other library functions. In this case, it would not be practical or advisable to redefine functions all within the EIG function. Instead, when you use/copy the EIG function, the other functions are copied as well: HESS, QR, etc.
Optional LAMBDA Arguments
In Excel, you can make an argument optional by enclosing it within square brackets. You can then use ISOMITTED or ISBLANK to check whether an argument was supplied and give it a default value.
=LAMBDA(value,[option], LET( option, IF( ISOMITTED(option), default, option ) ... ))
Examples of functions within the LAMBDA Library that use optional arguments include ONES, FLIP, SFROUND, and others.
Google Sheets does not (yet?) have an ISOMITTED function and does not permit optional arguments. However, arguments can be blank, so ISBLANK(...) often works fine for checking the initial value of a function argument.
Creating FOR Loops with LAMBDA Helper Functions
There are a few new built-in functions that are known as "lambda helper functions," including BYROW, BYCOL, MAP, and MAKEARRAY. These functions make it easy to apply a lambda function to a range of cells. More importantly, they can be thought of as a type of For Loop!
FOR EACH row IN array DO LAMBDA(row, expression)
=BYROW(array, LAMBDA(row, expression ))
The following example loops through each row in the given array, returning the sum of the row. The result is an mx1 array where m is the number of rows in the array.
[ 1 2 3
10 20 30
100 200 300]
=LET(
array,{1,2,3; 10,20,30; 100,200,300},
BYROW(array,LAMBDA(row, SUM(row) ))
)
Result: {6;60;600}
The name you use for row is up to you. See below for an example using BYROW as a loop like "FOR i = 3 TO 5".
FOR EACH column IN array DO LAMBDA(column, expression)
=BYCOL(array, LAMBDA(column, expression) )
Remember that BYCOL is essentially looping through the columns of the array, passing each column to the LAMBDA function one at a time. But, you can still access the array parameter within the LAMBDA expression if you want to.
[ 1 2 3
10 20 30
100 200 300]
=LET(
array,{1,2,3; 10,20,30; 100,200,300},
BYCOL(array,LAMBDA(column, SUM(column) ))
)
Result: {111,222,333}
FOR EACH cell IN array DO LAMBDA(cell, expression)
=MAP(array, LAMBDA(cell, expression))
=LET(
array,{1,2,3;10,20,30;100,200,300},
MAP(array,LAMBDA(cell, cell*2 ))
)
Result: {2,4,6;20,40,60;200,400,600}
I'm often tempted to use MAP when I want to use array indices, but that isn't how it works. If you give it a range like A140:C150, it passes each cell as a reference. So if you use ROW(cell) in the expression, it will give you the row number from the worksheet but not the relative row number from the array. Use MAKEARRAY (see below) to work with indices.
FOR i = 3 to 5 DO LAMBDA(i, expression)
This is really just the same as using BYROW, except that you can use SEQUENCE or SE to create the array that represents all values of i: {3;4;5}.
=LET(
array, {3;4;5},
BYROW(array,LAMBDA(i, i^2 ))
)
Result: {9;16;25}
Unlike a traditional for loop, there is not a way to break out of BYROW early. It will loop through every row in the array, and the size of the column that is returned by BYROW will be the same number of rows as the original array. However, within your expression you could return blank values with "" and then use FILTER to remove the blank values.
LOOP Through Elements of an Array While Accessing Row and Column Indices
=MAKEARRAY(rows, columns, LAMBDA(i, j, expression) )
The MAKEARRAY function is another LAMBDA helper function. The two parameters sent to the LAMBDA function are the row and column indices which we typically name "i" and "j". Note that by using MAKEARRAY within LET, we can access the value of each element in the array by the indices using INDEX(array,i,j).
=LET(
array,{1,2,3;10,20,30;100,200,300},
MAKEARRAY(ROWS(array),COLUMNS(array),
LAMBDA(i, j,
val, INDEX(array,i,j),
i & ":" & j & "=" & val
)
)
)
Result:
{"1:1=1","1:2=2","1:3=3";"2:1=10","2:2=20","2:3=30";"3:1=100","3:2=200","3:3=300"}
There are a couple of significant limitations to using BYROW, BYCOL, MAP and MAKEARRAY as general "for loops":
- The result of each expression can only be a single value
- They do not allow accumulator variables. Or in other words, they cannot change the values of other variables outside the scope of the LAMBDA expression.
On the topic of computational efficiency, I do not know if Microsoft made these functions parallelizable. However, because they do not use recursion or accumulators, they should be parallelizable. Although you can think of them as performing the expression in sequence like a typical for loop, in theory they could be performing all instances of the loop simultaneously (in parallel).
For more powerful (though not necessarily more efficient) coding options, we'll learn about LAMBDA recursion and the REDUCE and SCAN functions next.
Recursion with LAMBDAs
The truly powerful feature of the LAMBDA function is the ability to do recursion, which means that the function can call itself. By calling itself, you can use the results of the function as the inputs to call the function again. This enables iterative functions that might not be possible to do otherwise.
Besides other arguments that you might need, a recursive function usually consist of the following:
- An incrementer: The function must have a way to break the loop, so this could involve checking the value of an incrementer, incrementing until a value is sufficiently close to zero, or other methods.
- An accumulator: Most practical needs for recursion involve iteration and returning some final value other than the incrementer, so an accumulator argument fulfills that role.
The FACT function is already avilable for calculating the factorial of a number, but we will use factorial as a very simple recursion example. The factorial of 5 is 5*4*3*2*1.
Our function RE_FACT(n) will use n as the incrementer. Each call to RE_FACT will decrease the value of n by 1.
The accumulator will be an [optional] parameter so that we don't need to specify the starting value. The default starting value will be 1 because each successive value multiplies the accumulator by the current value of n.
/** * Recusive Factorial, RE_FACT(5) */ RE_FACT =LAMBDA(n,[accumulator], LET( accumulator,IF(ISOMITTED(accumulator),1,accumulator), IF(n<=0, accumulator, RE_FACT(n-1, n*accumulator) ) ));
Notice that the check to break out of the recursion is n<=0. When n reaches zero we return the current value of accumulator. Otherwise, we call the function again using the new value for n and the accumulator.
Recursion is complicated! So, if you have a hard time wrapping your brain around this, don't feel bad. Debugging recursive functions is also very difficult. You may be thinking "and this was a 'very simple' example?" Yeah, well the point is to understand the idea of accumulators. You can skip ahead to the REDUCE section if you want.
This is another example only for demonstration, because using recursion to sum the values in a vector is completely unnecessary and inefficient when compared to the SUM function. This function does allow us to test the recursion limit, which for this function is 2729.
/** * Recursive Sum Example, RE_SUM(SEQUENCE(10)) = 1+2+3+4+5+6+7+8+9+10 */ RE_SUM =LAMBDA(vector,[i],[acc], LET( i,IF(ISOMITTED(i),1,i), acc,IF(ISOMITTED(acc),0,acc), IF(i>ROWS(vector), acc, RE_SUM(vector, i+1, acc+INDEX(vector,i) ) ) ));
In this example, we have one fixed parameter (vector), an incrementer (i) that is used as the index to get the value from the vector, and an accumulator (acc) for storing the cumulative sum.
Using LET like this example is a convenient way of handling the defaults for the optional parameters.
I've tried to set up this example so it can be used like a code template for something more complicated. However, if you think that your function is going to need recursion ... make sure to consider REDUCE first.
Ideas for Accumulators
You can get creative in what you use for an accumulator variable. So far, these techniques have allowed me to use REDUCE in every case where I thought I needed recursion.
Arrays: You can use VSTACK and HSTACK to assemble an accumulator that stores multiple arrays or values.
Multiple Incrementers: You could use a single array argument to store multiple incrementers, then access those values using INDEX(acc,1) and INDEX(acc,2).
REDUCE as the Ultimate For Loop
Many (most?) iterative functions that you think would require recursion can likely be done using the REDUCE or SCAN functions. You can think of these functions as recursive LAMBDA helper functions that are not limited to 1024 or 2729 or 212 iterations, or whatever the number is that gives a #NUM error.
These may be the closest thing to a true For Loop in the sense that you can define and store any amount of information in the accumulator (up to computer memory limits, value size limits, etc.). It's just a matter of how clever you get with assembling (and disassembling) the accumulator.
FOR EACH value IN array DO LAMBDA(accumulator, value, new_accumulator)
=REDUCE(initial_accumulator, array, LAMBDA(accumulator, value, new_accumulator))
The initial_accumulator does not actually need to be used but it will be passed to the LAMBDA function as the first value of accumulator. I usually use a counting sequence for the array parameter such as SEQUENCE(10) so that the value passed to the LAMBDA function is essentially an integer incrementer.
The expression used to return the new_accumulator value can be as complicated as you want and can even involve other REDUCE functions. Ultimately, after REDUCE has looped through every value in the array, it is the new_accumulator value that is returned as the result. The final new_accumulator value does not need to be the same size as your initial_accumulator.
We will start with changing the recursive factorial function above to use REDUCE. Note that our initial_accumulator value is 1. The array is the sequence of values from n to 1 (because we need to multiply 5*4*3*2*1). At each step, REDUCE calls the LAMBDA function with two parameters: the current value of the accumulator (acc) and the next value in the array (value). The expression is then the new value of the accumulator.
/** * Factorial using REDUCE, RE_FACTR(5) */ RE_FACTR = LAMBDA(n, LET( array,SEQUENCE(n,1,n,-1), // produces the array {n;n-1;n-2;...;2;1} REDUCE(1, array, LAMBDA(acc, value, acc*value)) ));
REDUCE defines the number of iterations by the number of values in the array, so there is no need for code to break out of the loop. Although REDUCE will proceed to execute the LAMBDA for every value in the array, you can use logic that will stop the change in the accumulator value at any time - and this would act effectively as breaking out of the loop.
It's also important to see that the array does not need to be used within the LAMBDA function. The value is passed (the value parameter in the LAMBDA can not be blank), but you might only be using the array to define the number of iterations.
The recursive sum example is even easier with REDUCE:
/** * Recursive Sum with REDUCE, RE_SUMR(SEQUENCE(50)) */ RE_SUMR = LAMBDA(vector, REDUCE(0,vector,LAMBDA(acc,value, acc+value)) );Remember that for computational efficiency, it is better to use parallelizable functions.
More REDUCE Examples
Below are some of the functions in the LAMBDA Library that use the REDUCE and/or SCAN functions.
- PASCAL : Uses both the REDUCE and SCAN functions to assemble Pascal's Triangle.
- QR : QR decomposition - it IS possible in Excel.
- COMBINR : Returns all combinations of values in an array, r at a time.
- POLYMULT : Polynomial multiplication
- CHOLESKY : Cholesky decomposition assembles a matrix one column at a time.
- TIMER : A utility function that allows you to time how long a function takes to run.
Wrapping and Utility Functions
This section will be for examples of function templates that act as wrappers for various purposes.
Calling a recursive function without showing the optional parameters: When using recursive functions, you may want to prevent the user from seeing the optional parameters that are only used for the recursion. To do this, you can define the recursive function using LET.
TIMER can be used to time how long it takes a function to run a number of times in sequence (because sometimes a function runs too fast to measure with Excel). It also provides an example of how to create your own LAMBDA "helper" function: a function that uses LAMBDA as a parameter (like BYROW, BYCOL, etc).
The MAP_IJ example below behaves similarly to MAKEARRAY, giving MAP the ability to access the array's indices. Using this idea, you could extend MAP to any number of arrays while still accessing the indices.
/** * Like MAP for a single array, but with access to array indices * Usage: =MAP_IJ(array, LAMBDA(cell,i,j, expression) ) */ MAP_IJ = LAMBDA(array,function, LET(doc,"https://www.vertex42.com/lambda/candidates.html", iMat,SEQUENCE(1,SEQUENCE(1,COLUMNS(array)),SEQUENCE(ROWS(array))), jMat,SEQUENCE(SEQUENCE(ROWS(array)),1,SEQUENCE(1,COLUMNS(array))), res,MAP(array,iMat,jMat,LAMBDA(cell,i,j, function(cell,i,j) )), res ));
