POLYDER Function for Excel

=POLYDER(coeffs)

Argument	Description	Example
coeffs	Coefficients as a row vector in decreasing order of power	{1,-2,53}

Download the Template

In the template file, navigate to the Polynomials worksheet to see the POLYDER function in action.

Description

For the polynomial defined as p(x) = β_n*x_n + β_n-1*x_n-1 + … + β₂*x₂ + β₁*x₁ + β₀, the coeffs parameter should be a row vector: {β_n,β_n-1,...,β₁,β₀}.

The derivative of a polynomial is fairly simple to calculate just from the row vector of coefficients. For example, the derivative of β_nxⁿ is nβ_nx^(n-1). The derivative of a polynomial is therefore another polynomial one degree smaller.

POLYDER calculates the derivative of a polynomial by multiplying the sequence of powers by the coefficients:

For a polynomial of degree n=3:
powers = {3,2,1}
coeffs = {β₃,β₂,β₁}
p'(x) = powers*coeffs = {3β₃,2β₂,1β₁}

POLYDER returns a row vector of coefficients representing the derivative as a polynomial, or a separate row for each derivative if the original array contains multiple polynomials (as in the image below).

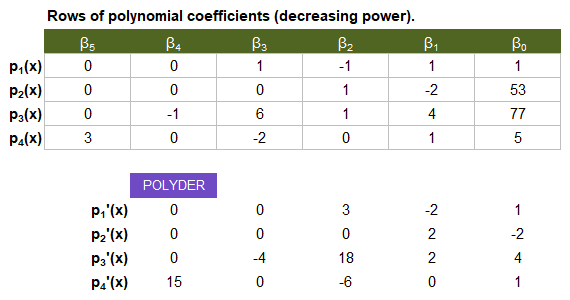
The derivative of a curve at a point is the tangent or slope of the curve at that point. The derivative is essentially a rate of change at that point. This applies to many areas of finance, physics, engineering, statistics, and science in general. Here are some examples of its use:

Physics: If a curve for position vs. time has been modeled as a polynomial, then POLYDER can return the polynomial representing the velocity vs. time. The second derivative represents the acceleration vs. time.
Statistics: For linear regression where data is fit using a polynomial (POLYFIT), the derivatives can aid in optimization and sensitivity analysis.

Lambda Formula

This code for using POLYDER in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

Code to Create Function via the Name Manager

Name: POLYDER
Comment: Returns the derivative of a polynomial
Refers To:

=LAMBDA(coeffs,
LET(doc,"https://www.vertex42.com/lambda/polyder.html",
    n,COLUMNS(coeffs)-1,
    powers,SEQUENCE(1,n+1,n,-1),
    CHOOSECOLS(coeffs*powers,SEQUENCE(n))
))

Code for AFE Workbook Module (Excel Labs Add-in)

/**
* Returns the derivative of the polynomial defined by coefficients in descending order of power.
*/
POLYDER = LAMBDA(coeffs,
LET(doc,"https://www.vertex42.com/lambda/polyder.html",
    n,COLUMNS(coeffs)-1,
    powers,SEQUENCE(1,n+1,n,-1),
    CHOOSECOLS(coeffs*powers,IF(n=0,1,SEQUENCE(n)))
));

Named Function for Google Sheets

Name: POLYDER
Description: Returns the derivative of a polynomial
Arguments: coeffs
Function:

LET(doc,"https://www.vertex42.com/lambda/polyder.html",
    n,COLUMNS(coeffs)-1,
    powers,SEQUENCE(1,n+1,n,-1),
    CHOOSECOLS(ARRAYFORMULA(coeffs*powers),IF(n=0,1,SEQUENCE(n)))
)

POLYDER Examples

Example

Evaluate the derivative of a polynomial defined as x^3 - 3x^2 - 2x + 53. Define the coeffs vector and the corresponding powers vector. After multiplying coeffs*powers, drop the last column.

Test: Copy and Paste this LET function into a cell
=LET(
    coeffs, {1,-3,-2,53},
    powers, {3, 2, 1, 0},
    deriv, DROP(coeffs*powers,,-1),
    deriv
)

Result: {3,-6,-2}

Do this again, but with the POLYDER function.

=LET(
    coeffs, {1,-3,-2,53},
    POLYDER(coeffs)
)

Result: {3,-6,-2}

Change History

4/09/2024 - v1.0.11 - Updated to evaluate the derivative of a constant as 0

POLYDER