QR (QR Decomposition)

=QR(matrix)

Download the Template

In the template file, navigate to the Matrices worksheet to see the QR function in action.

Description

QR returns the QR decomposition of matrix A such that A = MMULT(Q,R), using the Householder transformation algorithm. The function returns {Q;R} which means Q is stacked vertically on top of R (see the image below). R is an upper-triangular matrix (zeros below the diagonal) and Q is an orthonormal matrix (orthogonal, plus the columns and rows are normalized).

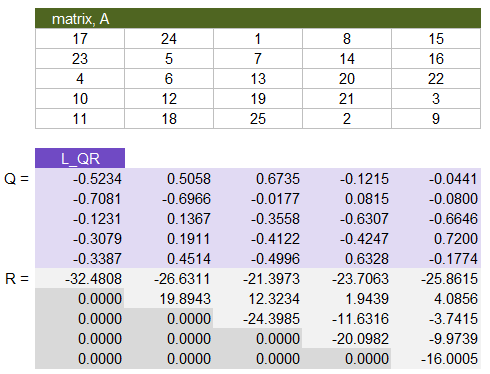
QR Decomposition is Important! It is used in solving linear systems, eigenvalue problems, signal processing, computer graphics, statistical methods, control theory and likely many other applications. It is the basis for the eigenvalue algorithm used in the function EIGENVALUE.

This version of the function may return results different from other QR algorithms, particularly the signs. I'm still trying to figure out why that is the case and what may be preferred, so if you're an expert and can explain how to improve the QR function, please contact me.

For educational purposes, I have included an Excel file below that includes both the QR function and examples worked out step by step. This is essentially the process I used to create and test the LAMBDA function. It also includes a function and examples that use the Gram-Schmidt algorithm. TIMER is used to test the computation time for the different algorithms.

⤓ qr-decomposition.xlsx

Until the introduction of the LAMBDA function (and specifically the REDUCE function), there wasn't a practical way to do QR decomposition in Excel with a single formula except using VBA. So, this is a pretty big step for spreadsheets.

Lambda Formula

This code for using QR in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

/**
* Returns the QR decomposition of matrix A using the Householder transformation process
* QR(matrix) returns {Q;R} (stacked vertically) where matrix=MMULT(Q,R).
*/
QR = LAMBDA(matrix,
LET(doc,"https://www.vertex42.com/lambda/qr.html",
    m,ROWS(matrix),n,COLUMNS(matrix),
    ks,SEQUENCE(n-1,1),
    Q3Q2Q1,REDUCE(SEQUENCE(n,n,0,0),ks,LAMBDA(acc,k,
        LET(   
            Ahat,IF(k=1,matrix,MMULT(acc,matrix)),
            ek,VSTACK(1,SEQUENCE(n-k,1,0,0)),
            xk,DROP(INDEX(Ahat,0,k),k-1),
            alpha,-SIGN(INDEX(xk,1))*SQRT(SUM(xk^2)),
            uk,xk-alpha*ek,
            vk,uk/SQRT(SUM(uk^2)),
            Qkhat,MUNIT(ROWS(ek))-2*MMULT(vk,TRANSPOSE(vk)),
            Qk,IF(k=1,Qkhat,
                VSTACK(
                HSTACK(MUNIT(k-1), SEQUENCE(k-1,n-k+1,0,0)),
                HSTACK(SEQUENCE(n-k+1,k-1,0,0), Qkhat))
                ),
            IF(k=1,Qk,MMULT(Qk,acc))
        )
    )),
    VSTACK(TRANSPOSE(Q3Q2Q1),MMULT(Q3Q2Q1,matrix))
));

Name: QR
Description: Returns the QR Decomposition of matrix A
Arguments: matrix
Function:

=LET(doc,"https://www.vertex42.com/lambda/qr.html",
    m,ROWS(matrix),n,COLUMNS(matrix),
    ks,SEQUENCE(n-1,1),
    Q3Q2Q1,ARRAYFORMULA(REDUCE(SEQUENCE(n,n,0,0),ks,LAMBDA(acc,k,
        LET(   
            Ahat,IF(k=1,matrix,MMULT(acc,matrix)),
            ek,VSTACK(1,SEQUENCE(n-k,1,0,0)),
            xk,L_DROP(INDEX(Ahat,0,k),k-1,0),
            alpha,-SIGN(INDEX(xk,1))*SQRT(SUM(xk^2)),
            uk,xk-alpha*ek,
            vk,uk/SQRT(SUM(uk^2)),
            Qkhat,MUNIT(ROWS(ek))-2*MMULT(vk,TRANSPOSE(vk)),
            Qk,IF(k=1,Qkhat,
                VSTACK(
                HSTACK(MUNIT(k-1), SEQUENCE(k-1,n-k+1,0,0)),
                HSTACK(SEQUENCE(n-k+1,k-1,0,0), Qkhat))
                ),
            IF(k=1,Qk,MMULT(Qk,acc))
        )
    ))),
    VSTACK(TRANSPOSE(Q3Q2Q1),MMULT(Q3Q2Q1,matrix))
)

QR Examples

Test: Copy and Paste this LET function into a cell
=LET(
    matrix, {12, -51, 4; 6, 167, -68; -4, 24, -41},
    QR(matrix)
)

Result (Q stacked on R): 
{ -0.8571,  0.3943,  0.3314;
  -0.4286, -0.9029, -0.0343;
   0.2857, -0.1714,  0.9429;

      -14,     -21,      14;
        0,    -175,      70;
        0,       0,     -35}

See Also

MAGNITUDE, DOT Product