QUADRATIC
=QUADRATIC(a,b,c) =QUADRATIC(coeffs)
| Argument | Description | Example |
|---|---|---|
| a | The coefficient of the x^2 term OR the row vector of coefficients {a,b,c} | 2 |
| b | The coefficient of the x term OR blank | 9 |
| c | The constant term OR blank | -5 |
| coeffs | The coefficients of the 2nd order polynomial as a row vector | {2,9,-5} |
Description
The QUADRATIC function returns the real or complex roots of a quadratic equation that is in the form \(ax^2 + bx + c = 0\). In Excel, this works with either the syntax QUADRATIC(coeffs) where coeffs is a row vector of polynomial coefficients {a, b, c}, or as QUADRATIC(a,b,c). The roots are returned as a 2x1 column vector {rmax; rmin}.
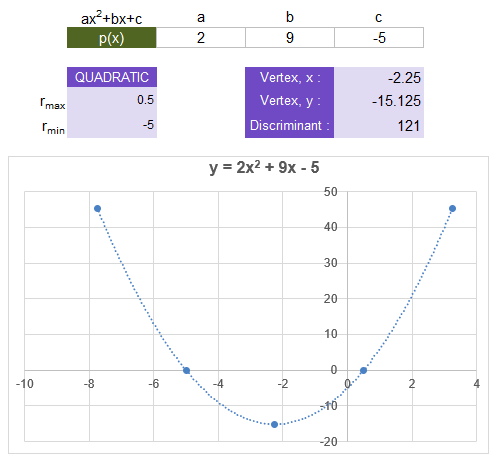 Example from the Lambda Library template file.
Example from the Lambda Library template file.If the roots are real numbers, it means that the parabola either crosses the x-axis in two places (discriminant>0) or the vertex is on the x-axis (discriminant=0) resulting in a repeated root: rmax=rmin.
If the roots are complex numbers, it means that the parabola does not touch or cross the x-axis. However, there are still 2 solutions to the equation, but they represent where the parabola intersects the imaginary axis in the complex plane. Google "visualize complex roots of the quadratic equation" for more information.
Assuming that a≠0, the two solutions to \(ax^2 + bx + c = 0\) are given by the quadratic formula and are typically written as: $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$$
The QUADRATIC function calculates the roots using the following form of the equation:
$$x = {\frac{-b}{2a} \pm \sqrt{ \left(\frac{b}{2a}\right)^2 - \frac{c}{a}}}$$This form is convenient for a few reasons:
1. The vertex of a parabola is located at \(x = -b/(2a)\)
2. We can reuse the calculation of the vertex within the radicand as follows:
vertex = -b/(2*a) radicand = vertex^2 - c/a pm = SQRT( ABS(radicand) )
3. The radicand in this form has the same properties as the discriminant \((b^2-4ac)\). Namely: if it is positive there are 2 distinct real roots. If it is zero there is one real repeated root. If it is <0 there are two complex roots which are conjugates of each other.
4. The two real roots are vertex+pm and vertex-pm.
5. Without any additional arithmetic, the complex roots will be COMPLEX(vertex,pm) and COMPLEX(vertex,-pm)
Cancelation Errors: For real roots, when |vertex|≈pm (very close to the same magnitude), then the root that is close to zero from the subtraction can have a significant cancelation error. This occurs when the magnitude of the vertex is much larger than the magnitude of c/a (when c≠0). To avoid this error, we can use the following identity to solve for the other real root:
rmin = (c/a)/rmax
Lambda Formula
This code for using QUADRATIC in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.
Code for AFE Workbook Module (Excel Labs Add-in)
/** * Quadratic Formula returns the real or complex roots of ax^2+bx+c=0 */ QUADRATIC = LAMBDA(a,[b],[c], LET(doc,"https://www.vertex42.com/lambda/quadratic.html", b,IF(ISOMITTED(b),INDEX(a,2),b), c,IF(ISOMITTED(c),INDEX(a,3),c), a,IF(COLUMNS(a)>1,INDEX(a,1),a), vertex,-b/(2*a), radicand,(vertex)^2-c/a, pm,SQRT(ABS(radicand)), rmax,vertex+pm, rmin,vertex-pm, IF(radicand>=0, IF(radicand=0,VSTACK(rmax,rmax), IF(vertex>=0, VSTACK(rmax,(c/a)/(rmax)), VSTACK((c/a)/rmin,rmin) ) ), VSTACK(COMPLEX(vertex,pm),COMPLEX(vertex,-pm)) ) ));
Named Function for Google Sheets
Name: QUADRATIC Description: Quadratic Formula - Returns either real or complex roots of ax^2+bx+c=0 Arguments: start, end, n (see above for descriptions and example values) Function: LET(doc,"https://www.vertex42.com/lambda/linspace.html", ARRAYFORMULA(start+(end-start)*(SEQUENCE(n)-1)/(n-1)) )
QUADRATIC Examples
Test: Copy and Paste this LET function into a cell =LET( coeffs, {2,9,-5}, QUADRATIC(coeffs) ) Result: {0.5; -5}
- [1] Golub, G. H. and Van Loan, C. F., Matrix Computations (4th ed.), p. 97, (The John Hopkins University Press, 2013)
- [2] Accurate Quadratic
- [3] Wikipedia: Quadratic Formula
