PPDER

=PPDER(pp_array)

Download the Template

In the template file, navigate to the Polynomials worksheet to see the PPDER function in action.

Description

PPDER returns the derivative of a piecewise polynomial as another piecewise polynomial. Each derivative of a polynomial reduces the degree by one, so the pp_array returned by PPDER(pp_array) will have one less column of coefficients.

The derivative of a polynomial can be calculated using the POLYDER function, so finding the derivative of an entire piecewise polynomial is simply a matter of finding the derivative of each individual segment and assembling a new piecewise polynomial structure.

pp_array structure: A piecewise polynomial is defined within the bounds [x₁,x_N] where the first column of the data structure array is the column vector of N break points. The other columns are the coefficients for each polynomial segment. The following example is a piecewise polynomial data structure described within the PPVAL function documentation.

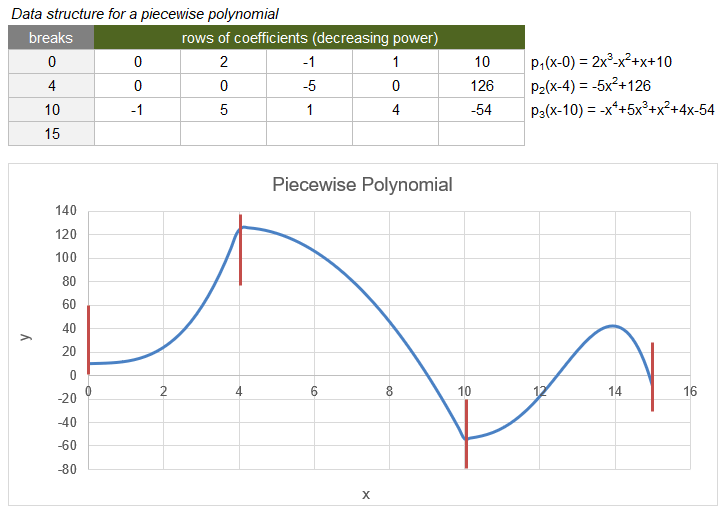
PPDER Example

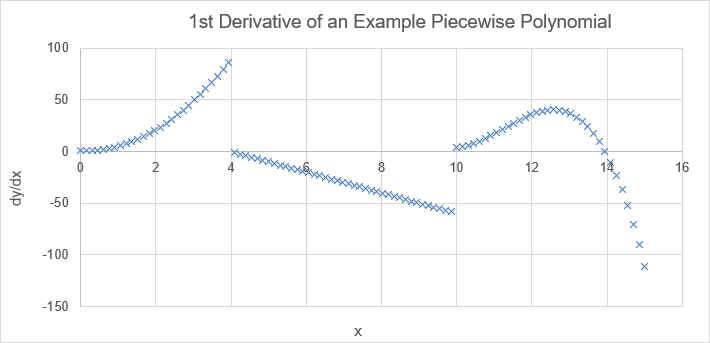
The following example graphs the first derivative of the piecewise polynomial shown above. Note that in this case the first derivative is not continuous.

=LET(
    pp_array, HSTACK({0;4;10;15},{0,2,-1,1,10; 0,0,-5,0,126; -1,5,1,4,-54}),
    xs, LINSPACE(0,15,100),
    dydx, PPVAL(PPDER(pp_array),xs)
)
Result: (see graph below)

See the example below showing the use of PPDER with cubic splines.

Lambda Formula

This code for using PPDER in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

/**
* Returns the derivative of a Piecewise Polynomial as another piecewise polynomial
*/
PPDER = LAMBDA(pp_array,
LET(doc,"https://www.vertex42.com/lambda/ppder.html",
    breaks,INDEX(pp_array,0,1),
    pieces,ROWS(breaks)-1,
    coeffs,DROP(pp_array,-1,1),
    newcoeffs,REDUCE(0,SEQUENCE(pieces),LAMBDA(acc,i,LET(
        deriv,POLYDER(CHOOSEROWS(coeffs,i)),
        IF(i=1,deriv,VSTACK(acc,deriv))
    ))),
    MAP(HSTACK(breaks,newcoeffs),LAMBDA(cell,IFERROR(cell,"")))
));

Name: PPDER
Description: Returns the Derivative of a Piecewise Polynomial
Arguments: pp_array
Function:
[in the works]

PPDER Examples

Example: First and Second Derivative of a Cubic Spline

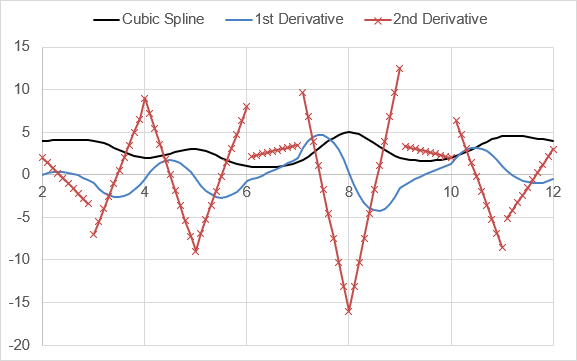
The CSPLINE function creates a cubic spline that has a continuous first derivative. Consider the following example from the CSPLINE documentation:

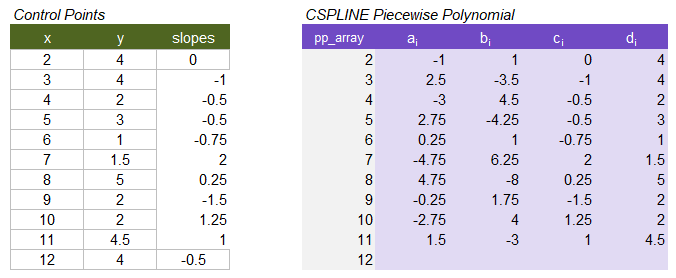Example control points and resulting cubic piecewise polynomial array

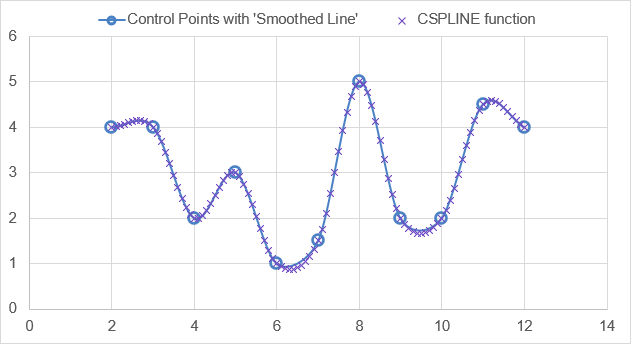Comparison of CSPLINE with the "Smoothed Line" option in Excel

Using LINSPACE, PPDER and PPVAL like above, we can graph the first and second derivatives of this example cubic spline. We can see that it is indeed C¹ continuous (first derivative is continuous), but it is not C² continuous (second derivative is not continuous).

Example: First and Second Derivative of a Natural Cubic Spline

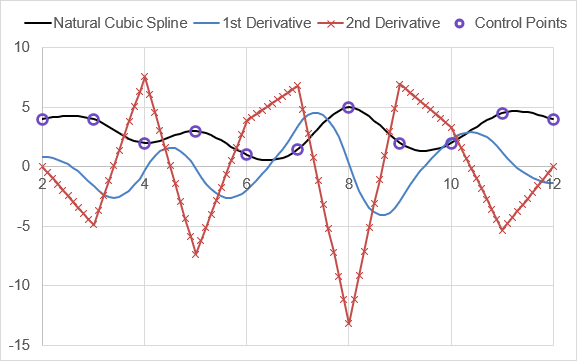
A Natural Cubic Spline is defined to be C² continuous. The following example is a natural cubic spline fit to the same points as the example above. Note that the second derivative is continuous in this case, and is zero at the end points.

=LET(
    x_cpts, {2;3;4;5;6;7;8;9;10;11;12},
    y_cpts, {4;4;2;3;1;1.5;5;2;2;4.5;4},
    pp_spline, NSPLINE(x_cpts,y_cpts),
    x_interp, LINSPACE(2,12,101),
    y_interp, PPVAL(pp_spline,x_interp),
    dy_interp, PPVAL( PPDER(pp_spline),x_interp),
    d2y_interp, PPVAL( PPDER(PPDER(pp_spline)),x_interp),
    HSTACK(x_interp,y_interp,dy_interp,d2y_interp)
)

Result: (see graph below)

See Also

PPVAL, CSPLINE, PPINT, POLYDER