TRAPZ
=TRAPZ(y, [x], [dx], [cumulative])
| Argument | Description | Example |
|---|---|---|
| y | A column vector of y values (or a matrix of column vectors) | {1;2;3} |
| x | (default=blank) A column vector of corresponding x values | blank |
| dx | (default=1) If x and dx are blank, then Δx is assumed to be 1. Only used if x is blank. | 1 |
| cumulative | (default=FALSE) If TRUE, returns intermediate cumulative values | FALSE |
In the template file, navigate to the Calc worksheet to see the TRAPZ function in action.
Description
TRAPZ is a numerical integration function that uses the Trapezoidal Rule [1] to approximate a definite integral from a set of ordered (x,y) values. If the x values are not given, you can either specify a value for dx, or leave it blank to assume unit spacing, Δx=1.
For our examples we'll use the polynomial function \(p(x)=-0.5x^3+5x^2-10x+10\). The image below shows a graph of 4 points between x=0 and x=6, with uniform spacing Δx=2. We'll use the trapezoidal rule to approximate the definite integral \(\int_0^6p(x)dx\). The approximation of the integral is the area shown in purple.
The trapezoidal rule uses a linear approximation between each point which sometimes overestimates and sometimes underestimates the true area under the curve. The area (integral) of each separate interval \([x_i,x_{i+1}]\) is:
$$\int_{x_i}^{x_{i+1}}p(x)dx\approx \frac{1}{2}(p(x_{i+1})+p(x_i))(x_{i+1}-x_i)$$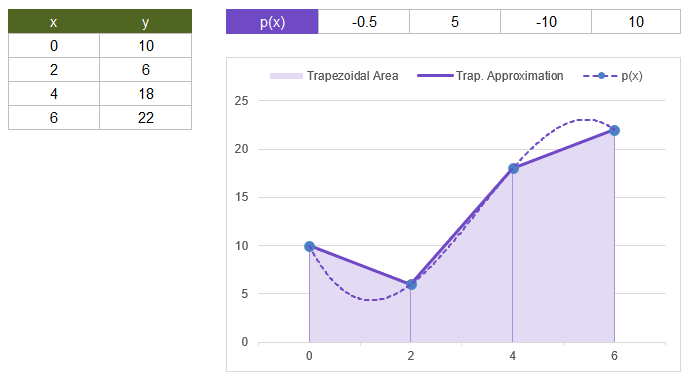
We can use POLYINT to calculate the exact integral for this polynomial example:
=LET(
px, {-0.5, 5, -10, 10},
pxint, POLYINT(px),
DIFF(POLYVAL(pxint,{0;6}))
)
Result: 78
Now we'll use TRAPZ to approximate the integral using the 4 points shown in the image above.
=LET(
x, {0;2;4;6},
y, {10;6;18;22},
TRAPZ(y,x)
)
Result: 80
TRAPZ(y,,2) would produce the same result because the x values have uniform spacing of Δx=2.
To get a more accurate approximation, we can use a smaller Δx interval. In the following example we're using 1000 intervals (1001 points) of size Δx=(6-0)/1000=0.006.
=LET(
x, LINSPACE(0,6,1001),
y, POLYVAL({-0.5,5,-10,10},x),
TRAPZ(y,x)
)
Result: 78.000018
When Y is a Matrix
This function is similar to the Matlab and NumPy trapz functions but it behaves a bit differently. When Y is a matrix, each of the column vectors in Y is integrated separately and the function returns a row vector (not a column vector) where each element is the integration of a column of Y.
To integrate a matrix Y by row instead of by column, use TRANSPOSE(Y).
If x is a vector, each column of Y uses the same x vector for the Δx spacing. If X is a matrix, then each column of Y uses the corresponding column of X. Each column is an independent integration.
The example below uses MESHGRID to create a 3D surface and TRAPZ to estimate the volume under the surface.
Cumulative Trapezoidal Integration
The updated function includes a cumulative option which if TRUE will return the intermediate values of the integral (a cumulative sum of the area under the curve). Remember that Excel starts array indexing at 1, so we use \(F(x_k)\) to represent the cumulative integral, with \(F(x_1)=0\). For k = 2 to N (where N is the number of values in vector y), we have:
$$ F(x_k) \approx \sum_{i=2}^{k} \frac{1}{2}(f(x_i)+f(x_{i-1}))(x_i-x_{i-1}) $$When the cumulative option is TRUE, the function returns the intermediate values as column vectors, so the size of the array that is returned is the same as the size of the input Y. This also works when Y and X are matrices - you just have to make sure to remember that TRAPZ integrates each column, so use TRANSPOSE as needed.
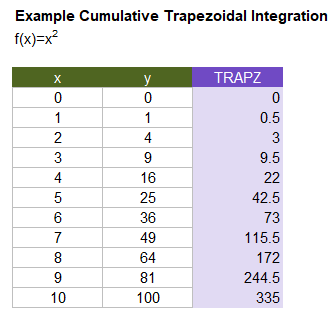
The following image is a screenshot from the Lambda Library template file showing the results of the second example below. Note that one of the benefits of trapezoidal integration is that the cumulative result is the same size as the x and y vectors, making it easy to set up for graphing.
Lambda Formula
This code for using TRAPZ in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.
Code for AFE Workbook Module (Excel Labs Add-in)
/** * Numerical Integration using the Trapezoidal Rule * Defaults: dx=1 if x and dx are blank, cumulative=FALSE */ TRAPZ = LAMBDA(y,[x],[dx],[cumulative], LET(doc,"https://www.vertex42.com/lambda/trapz.html", dx,IF(ISBLANK(dx),1,dx), areas,IF(ISOMITTED(x), (DROP(y,-1)+DROP(y,1))/2*dx, ((DROP(y,-1)+DROP(y,1))/2)*(DROP(x,1)-DROP(x,-1)) ), REDUCE("",SEQUENCE(COLUMNS(areas)), LAMBDA(acc,i,LET( col,CHOOSECOLS(areas,i), new,IF(cumulative=TRUE, SCAN(0,SEQUENCE(ROWS(col)+1), LAMBDA(acc,i,IF(i=1,0,acc+INDEX(col,i-1,1))) ), SUM(col) ), IF(i=1,new,HSTACK(acc,new)) )) ) ));
Named Function for Google Sheets
Name: TRAPZ Description: Numeric Integration using the Trapezoidal Rule Arguments: y, x, dx Function: =LET(doc,"https://www.vertex42.com/lambda/trapz.html", dx,IF(ISBLANK(dx),1,dx), areas,IF(ROWS(x)>1, ARRAYFORMULA(((L_DROP(y,-1,0)+L_DROP(y,1,0))/2)*(L_DROP(x,1,0)-L_DROP(x,-1,0))), ARRAYFORMULA((L_DROP(y,-1,0)+L_DROP(y,1,0))/2*dx) ), REDUCE("",SEQUENCE(COLUMNS(areas)), LAMBDA(acc,i,LET( col,CHOOSECOLS(areas,i), new,IF(cumulative=TRUE, SCAN(0,SEQUENCE(ROWS(col)+1), LAMBDA(acc,i,IF(i=1,0,acc+INDEX(col,i-1,1))) ), SUM(col) ), IF(i=1,new,HSTACK(acc,new)) )) ) )
TRAPZ Examples
Test: Copy and Paste this LET function into a cell =LET( xvec, LINSPACE(-2,2,101), yvec, LINSPACE(-3,3,201), X, MESHGRID(xvec),yvec,"X"), Y, MESHGRID(xvec),yvec,"Y"), Z, X^2-X*Y+Y^2, TRAPZ(TRANSPOSE(TRAPZ(TRANSPOSE(Z),xvec)),yvec) ) Result: 104.01
MESHGRID creates a matrix where each row is a different value of y and each column is a different value of x, so the size of Z in this example is 201x101. We integrated first by x using TRANSPOSE(Z) so that the columns represent constant y. The result of TRAPZ(TRANSPOSE(Z),xvec) is a 1x201 row vector (so we transpose the result to transform it to a 201x1 column vector). We then use TRAPZ again to integrate using yvec for the spacing.
To integrate first by y then by x:
=LET(
...
TRAPZ(TRANSPOSE(TRAPZ(Z,yvec)),xvec)
)
Result: 104.01
=LET(
x, LINSPACE(0,10,11),
y, x^2,
TRAPZ(y,x,,TRUE)
)
Result: {0; 0.5; 3; 9.5; 22; 42.5; 73; 115.5; 172; 244.5; 335}
See Also
DIFF, FDIFF, PDIFF, TRAPZ, SIMPSON
