PPINT - Piecewise Polynomial Integration in Excel

Work in Progress :: Please contact us to report errors, typos, etc.

=L_PPINT(pp_array, [a], [b])

Argument	Description	Example
pp_array	A piecewise polynomial (pp) data structure array	[see below]
a	(default=x₁) The lower limit for the integration	2
b	(default=x_N) The upper limit for the integration	8
cumulative	(default=FALSE) If TRUE, returns the cumulative integral corresponding to each segment	FALSE

Description

The definite integral of a polynomial, $P(x) = \int_a^bp(x)dx$, can be calculated exactly using L_POLYINT. Likewise, a Piecewise Polynomial, which is made up of separate polynomial segments, can be integrated exactly, using L_POLYINT on individual segments.

A piecewise polynomial is defined only within the bounds [x₁,x_N] where the first column of the data structure array is the column vector of N break points. For the purposes of integration, values outside that domain are considered to be zero.

The following example is a piecewise polynomial data structure described within the L_PPVAL function documentation.

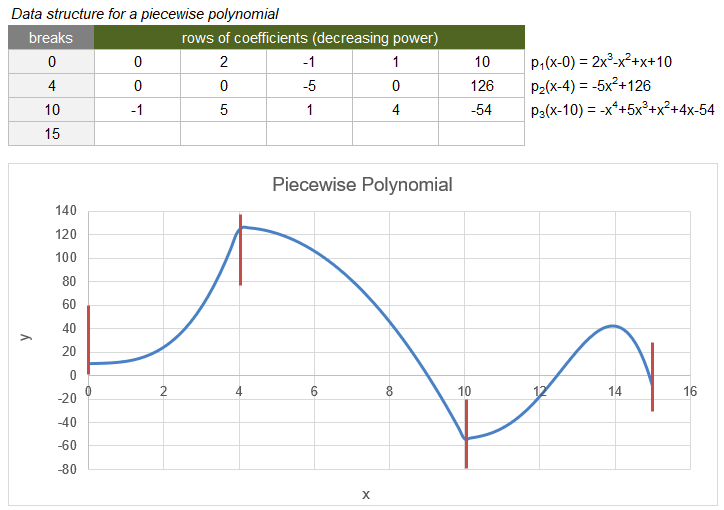
Data Structure for a Piecewise Polynomial in Excel

Integrating this example from a=-10 to b=100 is the same as integrating it from 0 to 15, since all values outside of [0,15] are treated as zero.

=LET(
    pp_array, {0,0,2,-1,1,10;4,0,0,-5,0,126;10,-1,5,1,4,-54;15,0,0,0,0,0},
    L_PPINT(pp_array)
)

Result: 528.5833

Cumulative Integration

If the optional cumulative parameter is TRUE, the function returns the cumulative integral corresponding to each segment where P(x₁)=0 and P(x_k) is:

$$ P(x_{k\ne1}) = \sum_{i=2}^{k} \int_a^bp_{i-1}(x)dx\ $$

If a and b are not specified, then the cumulative integral of the piecewise polynomial from a=x₁ to b=x_N is:

$$ P(x_{k\ne1}) = \sum_{i=2}^{k} \int_{x_{i-1}}^{x_i}p(x)dx\ $$

For the example above:

=LET(
    pp_array, {0,0,2,-1,1,10;4,0,0,-5,0,126;10,-1,5,1,4,-54;15,0,0,0,0,0},
    L_PPINT(pp_array,,,TRUE)
)

Result: {0; 154.667; 550.667; 528.5833}

Lambda Formula

This code for using L_PPINT in Excel is provided under the License as part of the LAMBDA Library, but to use just this function, you may copy the following code directly into your spreadsheet.

Code for AFE Workbook Module (Excel Labs Add-in)

/**
* Definite Integral of a Piecewise Polynomial from a to b
*/
L_PPINT = LAMBDA(pp_array,[a],[b],[cumulative],
LET(doc,"https://www.vertex42.com/lambda/ppint.html",
    breaks,INDEX(pp_array,0,1),
    pieces,ROWS(breaks)-1,
    coeffs,DROP(pp_array,-1,1),
    a,IF(OR(ISBLANK(a),a<INDEX(breaks,1)),INDEX(breaks,1),a),
    b,IF(OR(ISBLANK(b),b>INDEX(breaks,pieces+1)),INDEX(breaks,pieces+1),b),
    areas,SCAN(0,SEQUENCE(pieces+1),LAMBDA(acc,i,
    IF(i=1,0,LET(
        x_1,INDEX(breaks,i-1),
        x_2,INDEX(breaks,i),
        IF(NOT(AND(a<INDEX(breaks,i),b>INDEX(breaks,i-1))),acc+0,
            acc+L_POLYINT(CHOOSEROWS(coeffs,i-1),,MAX(0,a-x_1),MIN(b,x_2)-x_1)
        )
    )))),
    IF(cumulative=TRUE,areas,INDEX(areas,pieces+1,1))
));

Named Function for Google Sheets

Name: L_PPINT
Description: Integrate a Piecewise Polynomial
Arguments: pp_array, a, b, cumulative
Function:
[in the works]

L_PPINT Examples

Example: Integration of a Cubic Spline

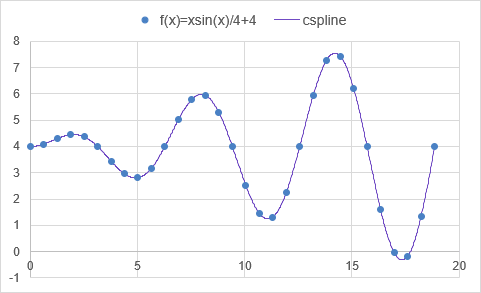
The L_CSPLINE function returns a cubic piecewise polynomial. For this example we'll use the function $f(x)=x\sin(x)/4+4$. The exact integral between 0 and 6π is (70.6858347...) so we'll see how well a cubic spline works with only 30 segments (31 points) beetween 0 and 6π. CSPLINE Example for PPINT

=LET(
    xs, L_LINSPACE(0,6*PI(),31),
    ys, xs/4*SIN(xs)+4,
    spline, L_CSPLINE(xs,ys),
    L_PPINT(spline)
)

Result: 70.706534
Error: 0.0207

The default cubic spline function calculates slopes using only forward, backward, and central difference approximations. But, we can improve the accuracy using L_PDIFF to obtain higher-order estimates of the slopes.

=LET(
    xs, L_LINSPACE(0,6*PI(),31),
    ys, xs/4*SIN(xs)+4,
    slopes, L_PDIFF(xs,ys,1,3),
    spline, L_CSPLINE(xs,ys,,slopes),
    L_PPINT(spline)
)

Result: 70.678297
Error: -0.0075

Note: The trapezoidal rule using L_TRAPZ for these same 31 points results in 70.8419 with an error of 0.156.

L_PPINT