Summary Statistics in Excel
[ Histogram ] ![]()
![]() [ Percentiles ]
[ Percentiles ]
In Part 4 of this series on Monte Carlo Simulation, we plotted the results of our Sales Forecast Example as a histogram to visualize the uncertainty in profit. Next, to provide a concise summary of the results, it is customary to report the mean, median, standard deviation, standard error, and a few other summary statistics to describe the results with numbers. The screenshot below shows these statistics calculated using simple Excel formulas.
Download the Sales Forecast Example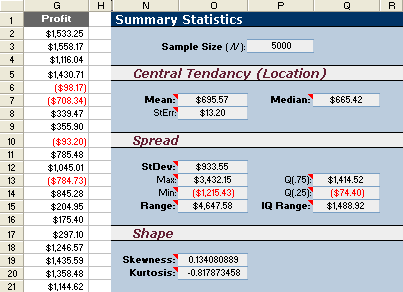
Figure 1: Summary statistics for the sales forecast example.
Statistics Formulas in Excel
Sample Size (n): =COUNT(G:G)
Sample Mean: =AVERAGE(G:G)
Median: =MEDIAN(G:G)
Sample Standard Deviation (s): =STDEV(G:G)
Maximum: =MAX(G:G)
Mininum: =MIN(G:G)
Q(.75): =QUARTILE(G:G,3)
Q(.25): =QUARTILE(G:G,1)
Skewness: =SKEW(G:G)
Kurtosis: =KURT(G:G)
Note: These Excel functions ignore text within the data set.
Sample Size (n)
The sample size, n, is the number of observations or data points from a single MC simulation. For this example, we obtained n = 5000 simulated observations. Because the Monte Carlo method is stochastic, if we repeat the simulation, we will end up calculating a different set of summary statistics. The larger the sample size, the smaller the difference will be between the repeated simulations. (See standard error below).
Central Tendancy: Mean and Median
The sample mean and median statistics describe the central tendancy or "location" of the distribution. The arithmetic mean is simply the average value of the observations.
The mean is also known as the "First Moment" of the distribution. In relation to physics, if the probability distribution represented mass, then the mean would be the balancing point, or the center of mass.
If you sort the results from lowest to highest, the median is the "middle" value or the 50th Percentile, meaning that 50% of the results from the simulation are less than the median. If there is an even number of data points, then the median is the average of the middle two points.
Extreme values can have a large impact on the mean, but the median only depends upon the middle point(s). This property makes the median useful for describing the center of skewed distributions such as the Lognormal distribution. If the distribution is symmetric (like the Normal distribution), then the mean and median will be identical.
Spread: Standard Deviation, Range, Quartiles
The standard deviation and range describe the spread of the data or observations. The standard deviation is calculated using the STDEV function in Excel.
The range is also a helpful statistic, and it is simply the maximum value minus the minimum value. Extreme values have a large effect on the range, so another measure of spread is something called the Interquartile Range.
The Interquartile Range represents the central 50% of the data. If you sorted the data from lowest to highest, and divided the data points into 4 sets, you would have 4 Quartiles:
Q1 or Q(0.25) is the First quartile or 25th percentile: =QUARTILE(G:G,1),
Q2 or Q(0.5) is the Median value or 50th percentile: =QUARTILE(G:G,2) or =MEDIAN(G:G),
Q3 or Q(0.75) is the Third quartile or 75th percentile: =QUARTILE(G:G,3),
Q4 is the Maximum value: =QUARTILE(G:G,4) or just MAX(G:G).
In Excel, the Interquartile Range is calculated as Q3-Q1 or:
The IQR is used in creating a box and whisker plot.
Shape: Skewness and Kurtosis
Skewness describes the asymmetry of the distribution relative to the mean. A positive skewness indicates that the distribution has a longer right-hand tail (skewed towards more positive values). A negative skewness indicates that the distribution is skewed to the left.
Kurtosis describes the peakedness or flatness of a distribution relative to the Normal distribution. Positive kurtosis indicates a more peaked distribution. Negative kurtosis indicates a flatter distribution.
Confidence Intervals for the True Population Mean
The sample mean is just an estimate of the true population mean. How accurate is the estimate? You can see by repeating the simulation (using F9 in this Excel example) that the mean is not the same for each simulation.
Standard Error
If you repeated the Monte Carlo simulation and recorded the sample mean each time, the distribution of the sample mean would end up following a Normal distribution (based upon the Central Limit Theorem). The standard error is a good estimate of the standard deviation of this distribution (the distribution of multiple mean values), assuming that the sample is sufficiently large (n >= 30).
The standard error is calculated using the following formula:
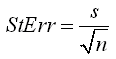
In Excel: =STDEV(G:G)/SQRT(COUNT(G:G))
95% Confidence Interval
The standard error can be used to calculate confidence intervals for the true population mean. For a 95% 2-sided confidence interval, the Upper Confidence Limit (UCL) and Lower Confidence Limit (LCL) are calculated as:
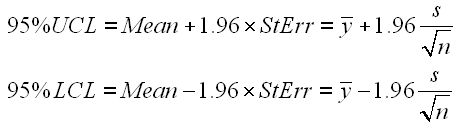
To get a 90% or 99% confidence interval, you would change the value 1.96 to 1.645 or 2.575, respectively. The value 1.96 represents the 97.5 percentile of the standard normal distribution. (You may often see this number rounded to 2). To calculate a different percentile of the standard normal distribution, you can use the NORMSINV() function in Excel.
Commentary
Keep in mind that confidence intervals make no sense (except to statisticians), but they tend to make people feel good. The correct interpretation: "We can be 95% confident that the true mean of the population falls somewhere between the lower and upper limits." What population? The population we artificially created! Lest we forget, the results depend completely on the assumptions that we made in creating the model and choosing input distributions. "Garbage in ... Garbage out ..." So, I generally just stick to using the standard error as a measure of the uncertainty in the mean. Since I tend to use Monte Carlo simulation for prediction purposes, I often don't even worry about the mean. I am more concerned with the overall uncertainty (i.e. the spread).
[ Histogram ] ![]()
![]() [ Percentiles ]
[ Percentiles ]
REFERENCES:
- Spreadsheet Modeling and Decision Analysis, 4/e, by: Cliff Ragsdale, Georgia Southern University
- Popescu et al., 2003, "Monte Carlo Simulation using Excel for Predicting Reliability of a Geothermal Plant", International Geothermal Conference, Reykjavik, Sept. 2003, http://jardhitafelag.is/papers/PDF_Session_07/S07Paper047.pdf
- Eric W. Weisstein. "Standard Error." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/StandardError.html
