Monte Carlo Simulation Basics
[ Preface ] ![]()
![]() [ Sales Forecast Example ]
[ Sales Forecast Example ]
A Monte Carlo method is a technique that involves using random numbers and probability to solve problems. The term Monte Carlo Method was coined by S. Ulam and Nicholas Metropolis in reference to games of chance, a popular attraction in Monte Carlo, Monaco (Hoffman, 1998; Metropolis and Ulam, 1949).
Computer simulation has to do with using computer models to imitate real life or make predictions. When you create a model with a spreadsheet like Excel, you have a certain number of input parameters and a few equations that use those inputs to give you a set of outputs (or response variables).
This type of model is usually deterministic, meaning that you get the same results no matter how many times you re-calculate. [ Example 1: A Deterministic Model for Compound Interest ]

Figure 1: A parametric deterministic model maps a set of input variables to a set of output variables.
Monte Carlo simulation is a method for iteratively evaluating a deterministic model using sets of random numbers as inputs. This method is often used when the model is complex, nonlinear, or involves more than just a couple uncertain parameters. A simulation can typically involve over 10,000 evaluations of the model, a task which in the past was only practical using super computers.
Example 2: A Stochastic Model
By using random inputs, you are essentially turning the deterministic model into a stochastic model. Example 2 demonstrates this concept with a very simple problem.
In Example 2, we used simple uniform random numbers as the inputs to the model. However, a uniform distribution is not the only way to represent uncertainty. Before describing the steps of the general MC simulation in detail, a little word about uncertainty propagation:
The Monte Carlo method is just one of many methods for analyzing uncertainty propagation, where the goal is to determine how random variation, lack of knowledge, or error affects the sensitivity, performance, or reliability of the system that is being modeled.
Monte Carlo simulation is categorized as a sampling method because the inputs are randomly generated from probability distributions to simulate the process of sampling from an actual population. So, we try to choose a distribution for the inputs that most closely matches data we already have, or best represents our current state of knowledge. The data generated from the simulation can be represented as probability distributions (or histograms) or converted to error bars, reliability predictions, tolerance zones, and confidence intervals. (See Figure 2).
Uncertainty Propagation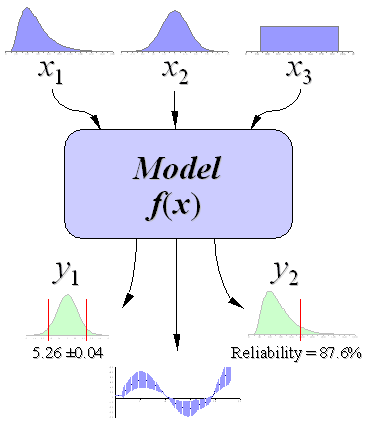
Figure 2: Schematic showing the principal of stochastic uncertainty propagation. (The basic principle behind Monte Carlo simulation.)
If you have made it this far, congratulations! Now for the fun part! The steps in Monte Carlo simulation corresponding to the uncertainty propagation shown in Figure 2 are fairly simple, and can be easily implemented in Excel for simple models. All we need to do is follow the five simple steps listed below:
Step 1: Create a parametric model, y = f(x1, x2, ..., xq).
Step 2: Generate a set of random inputs, xi1, xi2, ..., xiq.
Step 3: Evaluate the model and store the results as yi.
Step 4: Repeat steps 2 and 3 for i = 1 to n.
Step 5: Analyze the results using histograms, summary statistics, confidence intervals, etc.
On to an example problem ...
[ Preface ]![]()
![]() [ Sales Forecast Example ]
[ Sales Forecast Example ]
REFERENCES:
- Hoffman, P., 1998, The Man Who Loved Only Numbers: The Story of Paul Erdos and the Search for Mathematical Truth. New York: Hyperion, pp. 238-239.
- Metropolis, N. and Ulam, S., 1949, "The Monte Carlo Method." J. Amer. Stat. Assoc. 44, 335-341.
- Eric W. Weisstein. "Monte Carlo Method." From MathWorld--A Wolfram Web Resource.
- Paul Coddington. "Monte Carlo Simulation for Statistical Physics." Northeast Parallel Architectures Center at Syracuse University. http://www.npac.syr.edu/users/paulc/lectures/montecarlo/p_montecarlo.html
- Decisioneering.com. "What is Monte Carlo Simulation?"" Part of: Risk Analysis Overview - http://www.decisioneering.com/risk-analysis-start.html
