Discount Factor Table for Excel
A discount factor can be thought of as a conversion factor for time value of money calculations. The discount factor table below provides both the mathematical formulas and the Excel functions used to convert between present value (P), future worth (F), uniform gradient amount (G), and uniform series or annuity amount (A).
What is a Discount Factor?
Time value of money calculations are based on the principle that funds placed in a secure investment earn interest over time. The compounding principle states that if we have $P to invest now, the future value will increase to $F=$P*(1+i)n after n years, where i is the effective annual interest rate.
The discounting principle states that if we want to have $F in n years, we need to invest $P right now. So, discounting is basically just the inverse of compounding: $P=$F*(1+i)-n.
The discount formula can be written as P=F*(P/F,i%,n), where (P/F,i%,n) is the symbol used to define the discount factor. To convert the future value to the equivalent present value, you simply multiple the future value by the discount factor.
In the past, it was common to refer to a discount factor table to look up the number needed to perform a time value of money conversion. With the use of calculators and spreadsheets, the table lookup technique is practically obsolete.
Cash Flow Diagrams
A Cash Flow Diagram can help you visualize a series of receipts (positive values) and disbursements (negative values) at discrete periods in time. To be clear about the nomenclature used in the discount factor table, refer to the following cash flow diagrams for P, F, A, and G.

Fig 1. Present Value (single payment cash flow at t=0)

Fig 2. Future Worth (single payment cash flow at t=n)

Fig 3. Uniform Series Cash Flow (the same payment amount A from t=1 to t=n)

Fig 4. Uniform Gradient Series Cash Flow (linearly increasing payment amount from G at t=2 to (n-1)G at t=n
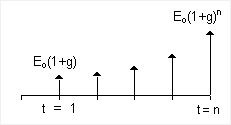
Fig 5. Exponential Gradient Series Cash Flow (g might be the inflation rate for example)
Discount Rate
The Discount Rate, i%, used in the discount factor formulas is the effective rate per period. It uses the same basis for the period (annual, monthly, etc.) as used for the number of periods, n. If only a nominal interest rate (rate per annum or rate per year) is known, you can calculate the discount rate using the following formula:
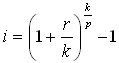
where
• r = nominal annual interest rate
• k = number of compounding periods per year
• p = number of periods per year corresponding to the basis for n
This formula for the effective rate per period is more general than the formula used in the Excel functions EFFECT and NOMINAL. The EFFECT and NOMINAL functions are only used for converting between the effective and nominal annual rates, where p=1.
Monthly Payment Periods (p=12)
If the compound period is also monthly, the discount rate for a monthly payment period (p=12) simplifies down to i = r / 12. To determine the discount rate for monthly periods with semi-annual compounding, set k=2 and p=12.
Daily Compounding (p=365 or p=360)
The above formula can be used to calculate an effective annual interest rate for daily compounding by setting p=1 and k to the number of banking days in the year (typically 365 or 360).
Discount Factor Table for Discrete Compounding
The following table lists discount factors used for conversions between common discrete cash flow series, present value, future worth, etc. The { } braces around the Excel formula indicate that the formula must be entered as an array function using Ctrl+Shift+Enter.
Example: To convert F to P, multiply F by the discount factor (P/F,i%,n). It might help to think of "P/F" as "P given F". This representation comes from the algebraic equivalence P=F*(P/F).
| Nomenclature | |
|---|---|
| i | Discount Rate (effective rate per period) |
| n | Number of Periods |
| P | Present Worth |
| F | Future Worth |
| A | Uniform Series Amount (or "Annuity") |
| G | Uniform Gradient Amount |
| Convert | Symbol | Discount Factor Formula | Discount Factor Formula in Excel |
|---|---|---|---|
| P to F | (F/P,i%,n) | (1+i)n | =FV(i,n,0,-1) |
| F to P | (P/F,i%,n) | (1+i)-n | =PV(i,n,0,-1) |
| F to A | (A/F,i%,n) | i/((1+i)n-1) | =PMT(i,n,0,-1) |
| P to A | (A/P,i%,n) | i*(1+i)n/((1+i)n-1) | =PMT(i,n,-1) |
| A to F | (F/A,i%,n) | ((1+i)n-1)/i | =FV(i,n,-1) |
| A to P | (P/A,i%,n) | ((1+i)n-1)/(i*(1+i)n) | =PV(i,n,-1) |
| G to P | (P/G,i%,n) | ((1+i)n-1)/(i2*(1+i)n)-n/(i*(1+i)n) | {=NPV(i,(ROW(INDIRECT("1:"&n))-1))} |
| G to F | (F/G,i%,n) | ((1+i)n-1)/i2-(n/i) | {=(P/G,i%,n) * (F/P,i%,n)} |
| G to A | (A/G,i%,n) | (1/i)-n/((1+i)n-1) | {=(P/G,i%,n) * (A/P,i%,n)} |
| EG to P | (P/EG,z-1,n) | (zn-1)/(zn(z-1)), z=(1+i)/(1+g) | =PV(z-1,n,-1) |
The Excel formulas for (F/G,i%,n) and (A/G,i%,n) are based on the algebraic equivalence of F/G=(P/G)*(F/P) and A/G=(P/G)*(A/P). Replace the discount factor symbols (P/G,i%,n), (F/P,i%,n) and (A/P,i%,n) with the appropriate discount factor formula listed in the table.
Discount Factors for Continuous Compounding
Continuous compounding is not exactly the same as daily compounding. The exact discount factor formulas for continuous compounding are given in the table below (where n is the number of years and r is the nominal annual rate). Note that the discount factor for F to P is just the inverse (1/x) of the factor for P to F.
| Convert | Symbol | Discount Factor Formula | ... in Excel |
|---|---|---|---|
| F to P | (P/F,r%,n) | e-r*n = 1/er*n | =1/EXP(r*n) |
| P to F | (F/P,r%,n) | er*n | =EXP(r*n) |
| F to A | (A/F,r%,n) | (er-1)/(er*n-1) | =(EXP(r)-1)/(EXP(r*n)-1) |
| A to F | (F/A,r%,n) | (er*n-1)/(er-1) | =(EXP(r*n)-1)/(EXP(r)-1) |
| P to A | (A/P,r%,n) | (er-1)/(1-e-r*n) | =(EXP(r)-1)/(1-1/EXP(r*n)) |
| A to P | (P/A,r%,n) | (1-e-r*n)/(er-1) | =(1-1/EXP(r*n))/(EXP(r)-1) |
See Also
Additional Resources
- Time Value of Money at wikipedia.com.
- Time Value Function Tutorial by Timothy R. Mayes at http://www.tvmcalcs.com/index.php/calculators/excel_tvm_functions/excel_tvm_functions_page1
- Discount Mathematics at http://www.excelexchange.com/discount%20mathematics.htm.