Negative Amortization Example

The purpose of this article is to answer the question "what is negative amortization?" and explain how it can arise in amortization calculations and amortization schedules. I'll try to illustrate the concept using a basic amortization table. For more information about the history of this term and how it applies to loans and mortgages, I recommend reading the articles listed at the bottom of this page.

Definition of Negative Amortization

Negative Amortization is the increase in Principal through the addition of unpaid interest.

Most definitions describe this as occurring when a payment is insufficient to cover the interest due, resulting in the interest being added to the loan balance.

The result of negative amortization is that you end up paying interest on your unpaid interest.

Example Amortization Table

The amortization table below illustrates how missing a payment results in interest added to the Principal (see the numbers highlighted red). In this example, the second monthly payment of a 30 year loan is skipped.

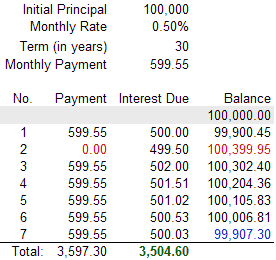
The interest due is calculated as the Monthly Rate * Previous Balance, so on Payment No. 3, you end paying even more interest than you did on your first payment. In the table, I summed the total payment and interest over the first 7 payments and highlighted the balance at the end of the 7th month in blue. In this example, it cost about $3000 to make up for the one missed payment (to bring the balance back to the amount after the first payment). This doesn't take into late fees or penalties.

Simple Interest Amortization

When handling missed payments, the alternative to negative amortization is "simple interest amortization", where the unpaid interest is NOT added to the Principal balance, but instead is accrued in a separate account to be paid off first before the Principal. The table below shows how simple interest amortization compares to the negative amortization example when the second payment is missed.

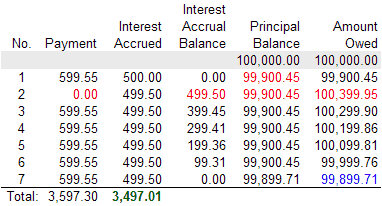
The thing to notice is that when the second payment is missed, the Principal balance stays the same, and therefore the interest due on payment No 3 is still only 499.50. The total amount owed still goes up, because you are going to have to pay off the interest that has accrued, but at least you aren't paying interest on interest.

Negative Amortization & Compound Interest

If "simple interest" is defined as paying interest on the principal only, then negative amortization is basically "compound interest" because it results in interest being paid on interest. I bring this up because if you are using my amortization schedule spreadsheet or other loan calculators and mortgage calculators that let you choose a compound period that is different than the payment period, you need to realize an important fact:

Negative Amortization can arise when calculating the effective rate per payment period if the compound period is shorter than the payment period.

When the compound period is different than the payment period, an amortization calculator often uses an effective interest rate, derived from the compound interest formula. For a description of this formula, see "Calculating the Rate Per Period". Such is the case with Canadian mortgages where the compound period is semi-annual and payments are usually made monthly. That's fine. Where you'd run into negative amortization is if you selected a Weekly Compound Period with a Monthly Payment Period (the weekly compound period being shorter than the monthly payment period).

When does this occur? I don't know. I've had many requests to add a daily compound period to my loan amortization schedule, so I complied. But, perhaps what people really are wanting is an amortization table that accrues interest daily as in a so-called "simple interest mortgage"?