Stochastic Model Example
[ Back to Monte Carlo Simulation Basics ] ![]()
A stochastic model is one that involves probability or randomness. In this example, we have an assembly of 4 parts that make up a hinge, with a pin or bolt through the centers of the parts. Looking at the figure below, if A + B + C is greater than D, we're going to have a hard time putting this thing together.
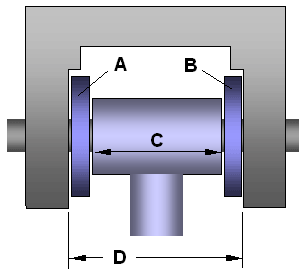
Figure 1: Schematic for a simple hinge.
Let's say we have a million of each of the different parts, and we randomly select the parts we need in order to assemble the hinge. No two parts are going to be exactly the same size! But, if we have an idea of the range of sizes for each part, then we can simulate the selection and assembly of the parts mathematically.
The table below demonstrates this. Each time you press "Calculate", you are simulating the creation of an assembly from a random set of parts. If you ever get a negative clearance, then that means the combination of the parts you have selected will be too large to fit within dimension D. Do you ever get a negative clearance?
This example demonstrates almost all of the steps in a Monte Carlo simulation. The deterministic model is simply D-(A+B+C). We are using uniform distributions to generate the values for each input. All we need to do now is press the "calculate" button a few thousand times, record all the results, create a histogram to visualize the data, and calculate the probability that the parts cannot be assembled.
Of course, you don't want to do this manually. That is why you use software (including Excel add-ins) to automate the Monte Carlo simulation.
