In Excel, an Array Formula allows you to do powerful calculations on one or more value sets. The result may fit in a single cell or it may be an array. An array is just a list or range of values, but an Array Formula is a special type of formula that must be entered by pressing Ctrl+Shift+Enter. The formula bar will show the formula surrounded by curly brackets {=...}.
Array formulas are frequently used for data analysis, conditional sums and lookups, linear algebra, matrix math and manipulation, and much more. A new Excel user might come across array formulas in other people's spreadsheets, but creating array formulas is typically an intermediate-to-advanced topic.
Download the Example File (ArrayFormulas.xlsx)
Topics and Examples in This Article:
- Entering an Array Formula
- Using Array Constants
- A Simple Array Formula Example
- Entering a Multi-Cell Array Formula
- Dynamic "Spillable" Arrays in Office365
- Nested IF Array Formulas
- COUNTIF Alternative: SUM-Boolean Array Formulas
- Multi-Criteria Boolean Array Formulas
- Sequential Number Arrays (1,2,3,...)
- Formulas for Matrices: MUNIT, MMULT, TRANSPOSE, etc.
- Other Array Formula Examples
Watch the Intro Video
Entering and Identifying an Array Formula
- When using an Array Formula, you press Ctrl+Shift+Enter instead of just Enter after entering or editing the formula. This is why array formulas are often called CSE formulas.
- An Array Formula will show curly brackets or braces around the formula in the Formula Bar like this: {=SUM(A1:A5*B1:B5)}
- Array Constants (arrays "hard-coded" into formulas) are enclosed in braces { } and use commas to separate columns, and semi-colons to separate rows, like this 2x3 array: {1, 1, 1; 2, 2, 2}
- If an Array Formula returns more than one value (a multi-cell array formula), first select a range of cells equal to size of the returned array, then enter your formula.
- To select all the cells within a multi-cell array: Press F5 > Special > Current Array.
! Every time you edit an Array Formula, you must remember to press Ctrl+Shift+Enter afterward. If you forget to, the formula may return an error without you realizing it.
NOTE Google Sheets uses the ARRAYFORMULA function instead of showing the formula surrounded by braces. It is not necessary to press Ctrl+Shift+Enter in Google Sheets, but if you do, ARRAYFORMULA( is added to the beginning of the formula.
Using Array Constants in Formulas
Many functions allow you use array constants like {1,2,6,12} as arguments within formulas. An example that I often use in my yearly calendar templates returns the weekday abbreviation for a given date. The nice thing about this formula is that you can choose whether to display a single character or two characters.
=INDEX({"Su";"M";"Tu";"W";"Th";"F";"Sa"},WEEKDAY(theDate,1))
This formula is not technically an Array Formula because you don't enter it using Ctrl+Shift+Enter. Using a hard-coded array within a formula does not necessarily require using Ctrl+Shift+Enter.
TIP If you are going to use the array constant in multiple formulas, you may want to first create a Named Constant. Go to Formulas > Name Manager > New Name, enter a descriptive name like payment_frequency and enter ={1,2,6,12} into the Refers To field. You can use the name within your formulas. If you ever want to change the values within that array constant, you only need to change it one place (within the Name Manager).
A Simple Array Formula Example
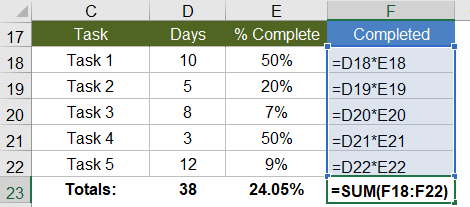
To start out, I will show how an array formula works using a very basic example. Let's say that I have a list of tasks, the number of days each of those tasks will take, and a column for the percent complete. I want to know the total number of days that have been completed.
Without an array formula, you would create another column called "Completed" and multiply the number of days by the % complete, and copy the formula down. Then I would use SUM to total the number of days completed, like the image below:
With an array formula, you can do essentially the same thing without having to create the extra column. Within a single cell, you can calculate the total days completed as =SUM(D18:D22*E18:E22), remembering to press Ctrl+Shift+Enter because it is an array formula.
{ =SUM(D18:D22*E18:E22) } Evaluation Steps Step 1: =SUM( {10;5;8;3;12} * {0.5;0.2;0.07;0.5;0.09} ) Step 2: =SUM( {10*0.5;5*0.2;8*0.07;3*0.5;12*0.09} ) Step 3: =SUM( {5;1;0.56;1.5;1.08} ) Step 4: =9.14
In this and other examples, I've shown the evaluation steps below the formula so that you can see how the formula works. You don't actually type the curly brackets { }, but in this article I will surround all array formulas with brackets to indicate that they are entered as CSE formulas.
In the evaluation steps shown in the above example, you'll see that Excel is multiplying each element of the first array by the corresponding element in the second array, and then SUM adds the results.
NOTE It turns out that this particular example can be used to show how the SUMPRODUCT function works, but the SUMPRODUCT function deserves its own article.
To take this example just a bit further, if all we wanted to know was the Total Percent Complete for the entire project, we can divide the total days completed (9.14) by the total days (38) all within a single array formula, and we don't need column F at all (as shown in the image below).
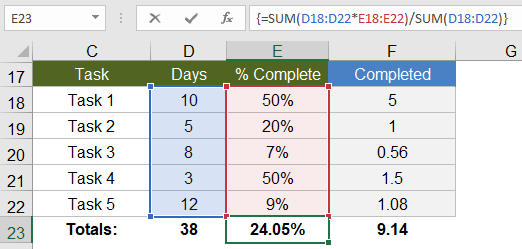
This example is an example of a single-cell array formula, meaning that the formula is entered into a single cell.
Entering a Multi-Cell Array Formula
Whenever your array formula returns more than one value, if you want to display more than just the first value, you need to select the range of cells that will contain the resulting array before entering your formula. Doing this will result in a multi-cell array formula, meaning that the result of the formula is a multi-cell array.
Using the same example as above, we could use an array formula in the Completed column to calculate Days * Percent Complete. First, select cells F18:F22, then press = and enter the formula, followed by Ctrl+Shift+Enter (CSE). The image below is what it will look like just before you press CSE.
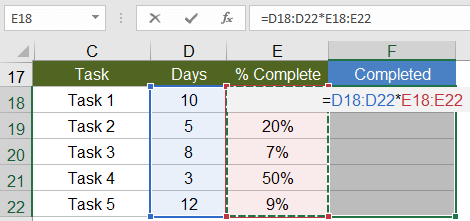
You can edit a multi-cell array formula by selecting any of the cells in the array and then updating the formula and pressing Ctrl+Shift+Enter when you are done. However, you can't use this technique to modify the size of the array.
"You can't change part of an array" - This is the warning or error you will get if you try to insert rows or columns or change individual cells within a multi-cell array.
Using multi-cell array formulas can make it more difficult to customize a spreadsheet because to change the size of the array requires that you (1) delete the formula (after selecting all the cells of the array), (2) select the new range of cells, and (3) re-enter the array formula. TIP: Make sure to copy your original formula before deleting it. Then, when you re-enter the formula, you can paste it and modify the ranges.
Dynamic Array Formulas
Office 365! This article was originally written before the new dynamic array formulas or "spillable" arrays were available. In Office 365, many of the formulas and functions no longer require the use of Ctrl+Shift+Enter. Some of the new functions, such as SEQUENCE, make the formulas in this article much easier. I have included some of these new examples, highlighted in purple.
Nested IF Array Formulas
A nested IF array formula can be very powerful and is probably one of the more common uses for array formulas in Excel. Although Excel provides the SUMIF and COUNTIF and AVERAGEIF functions, they don't allow as much freedom as a nested IF array formula.
MAX-IF Array Formula
Older versions of Excel do not have the MAXIFS or MINIFS functions, so let's create our own MAX-IF formula. When we use hyphens to name a formula, it usually means that we're nesting the functions (IF within MAX in this case).
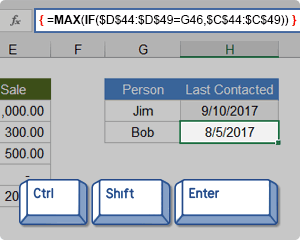
Let's say that I have the following contact and sales log and I want a formula that will tell me when I last contacted Bob (cell H51).
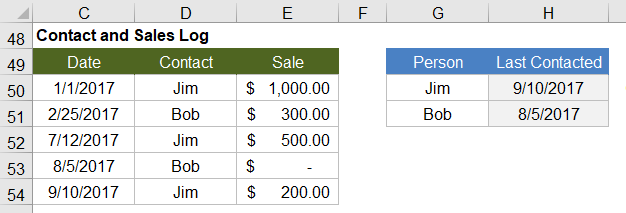
Using MAX on the date range will give me that latest date (9/10/2017), but I only want to include the rows where the contact is Bob. So, I'll use the MAX-IF array formula:
{ =MAX(IF(contact_range="Bob",date_range)) } Evaluation Steps Step 1: =MAX(IF({"Jim";"Bob";"Jim";"Bob";"Jim"}="Bob", date_range )) Step 2: =MAX(IF({FALSE;TRUE;FALSE;TRUE;FALSE}, date_range )) Step 3: =MAX( {FALSE,2/25/2017,FALSE,8/5/2017,FALSE} ) Step 4: =8/5/2017
LARGE-IF Array Formula
The LARGE and SMALL functions come in handy when you want to find the value that is perhaps the 2nd largest or 2nd smallest.
The following function will return the second largest sale where the contact is Jim.
{ =LARGE(IF(contact_range="Jim",sale_range),2) }
SMALL-IF Array Formula
This function returns the second smallest sale where the contact is Jim.
{ =SMALL(IF(contact_range="Jim",date_range),2) }
The LARGE and SMALL functions can be used for sorting arrays. More on that later. Hopefully, Excel will introduce a SORT function soon (Google Sheets has already done that).
The SMALL-IF formula can be used in combination with INDEX to do a lookup a value based on the Nth Match.
SUM-IF Array Formula
Yes, there is already a SUMIF function that is generally better than using an array formula, but we'll be getting into more advanced SUM-IF array formulas, so it's useful to see the simple example:
{ =SUM(IF(contact_range="Jim",sales_range)) }
More Reading: Chip Pearson provides some great examples of ways to use nested IF functions within the SUM and AVERAGE functions to ignore errors and zero values. See Chip Pearson's article.
COUNTIF Alternative: SUM-Boolean Array Formulas
Although there is already a COUNTIF function, the criteria available in the COUNTIF family of functions is limited. An alternative method is to do a SUM of boolean (TRUE/FALSE) results that have been converted to 0s and 1s (FALSE=0, TRUE=1). Boolean results can be converted to 0s and 1s by adding +0, multiplying by *1 and by using double negation.
SUM-ISERROR: Count the number of Error values in a range
{ =SUM(1*ISERROR(range)) } { =SUM(0+ISERROR(range)) } { =SUM(--ISERROR(range)) } Evaluation Steps Step 1: =SUM( 1*{FALSE,TRUE,TRUE,FALSE,TRUE} ) Step 2: =SUM( {0,1,1,0,1} ) Step 3: =3
SUM-ISBLANK: Count the number of Blank values in a range
{ =SUM(--ISBLANK(range)) }
Remember: A formula that returns an empty "" string is considered NOT blank.
SUM-NOT-ISBLANK: Count the number of Non-Blank values in a range
{ =SUM(--NOT(ISBLANK(range)) }
Multi-Criteria Boolean Array Formulas
The AND and OR functions return only a single value, even when they contain multiple arrays, so we don't generally use them within array formulas.
For multiple-criteria logical array formulas, such as SUM-IF between two dates, you need to do the boolean logic by adding boolean values for "or" conditions and by multiplying boolean values for "and" conditions.
SUM-IF Between Two Dates
Yes, SUMIFS would be easier, but let's assume we are using an older version of Excel. Referring back to the Contact and Sales log, we'll sum all of the Sales between 2/1/2017 and 9/1/2017, meaning that Date >= 2/1/2017 AND Date <= 9/1/2017.
{ =SUM(IF((date_range>=start)*(date_range<=end), sum_range) ) } Evaluation Steps Step 1: SUM(IF({FALSE,TRUE,TRUE,TRUE,TRUE}*{TRUE,TRUE,TRUE,TRUE,FALSE},sum_range)) Step 2: SUM(IF({0,1,1,1,0},sum_range)) Step 3: SUM({FALSE,300,500,0,FALSE}) Step 4: 800
In this case we don't need to use 1*(...) to convert the boolean values, because the boolean values are converted to 0s and 1s automatially when we multiply the two arrays together. The IF function in Excel treats the value 0 as FALSE and all other values as TRUE.
Overlapping OR Conditions
To demonstrate a logical OR condition, we'll sum the sales where Name = "Bob" OR Date > 7/1/2017. An "or" condition is true when one or more of the conditions is true, so we check whether the sum of the expressions is greater than 0.
{ =SUM(IF( ((contact_range="Bob")+(date_range>=date))>0, sum_range) ) } Evaluation Steps Step 1: SUM(IF(({FALSE,TRUE,FALSE,TRUE,FALSE}+{FALSE,FALSE,TRUE,TRUE,TRUE})>0,sum_range)) Step 2: SUM(IF({0,1,1,2,1}>0,sum_range)) Step 3: SUM(IF({FALSE,TRUE,TRUE,TRUE,TRUE},sum_range)) Step 4: SUM({FALSE,300,500,0,200}) Step 5: 1000
Using this approach, you can create multiple-criteria equivalents for MAX-IF, LARGE-IF, and other array formulas.
Sequential Number Arrays
For many array formulas, you will need to use an array of sequential numbers like {1; 2; 3; ... n}. You can return a sequential number array from 1 to n using this formula:
{ =ROW(1:n) } -or- { =ROW(OFFSET($A$1,0,0,n,1)) }
Important: Although it doesn't matter what is contained in cell A1, if you delete the cell (by removing row 1 or column A for example), insert a row above or a column to the left of cell A1, or cut and paste cell A1 to a different location, your array formula will be messed up. To avoid this problem, use the INDIRECT function:
{ =ROW(INDIRECT("1:"&n)) } -or- { ROW(OFFSET(INDIRECT("A1"),0,0,n,1)) }
NOTE The OFFSET and INDIRECT function are volatile functions. If calculation speed becomes a problem due to these formulas, you could either use ROW(1:n) and risk having row 1 removed, or you could reference a hidden or protected worksheet using =ROW(Sheet4!1:n)
Office 365! The new SEQUENCE function available in Office 365 makes creating sequential number arrays a lot easier. The above sequence starting with the default value of 1 is simply =SEQUENCE(n).
Variant #1: Create a Sequence of Whole Numbers from i to j
If you want to hard-code the values for i and j into the formula, an array formula such as ROW(4:8) may work fine to create the array {4;5;6;7;8}. If you want the formula to use cell references for i and j, you can use INDIRECT like this:
A1 = 4 B1 = 8 { =ROW(INDIRECT(A1&":"&B1)) } Result: {4;5;6;7;8}
In Office 365! =SEQUENCE(j-i+1,,i)
Variant #2: Create an n x 1 Vector of Whole Numbers Starting From s
You can use this technique when you want to specify the length of the number array instead of the end value. To create the array {s; s+1; s+2; ... s+n-1} use
s = 4 n = 7 { =s+ROW(OFFSET(INDIRECT("A1"),0,0,n,1))-1 } -or- { =ROW(INDIRECT(s&":"&s+n-1)) } Result: {4;5;6;7;8;9;10}
In Office 365! =SEQUENCE(n,,s)
Variant #3: Sequence of Dates Between START and END (inclusive)
To create an array of dates from start through end (assuming start and end are cells containing date values), remember that date values are stored as whole numbers. If they are indeed date values and not date-time values, you can use:
start_date = 1/1/2018 end_date = 1/5/2018 { =ROW(INDIRECT(start_date&":"&end_date)) } Result: {43101;43102;43103;43104;43105}
The result shows the numeric values for 1/1/2018, 1/2/2018, etc. You can format the results using whatever date format you want. If your start and end dates might be date-time values, then strip the time portion off of the number like this:
{ =ROW(INDIRECT(INT(start_date)&":"&INT(end_date)) }
In Office 365! =SEQUENCE(end_date-starte_date+1,,start_date)
Variant #4: Create an n x 1 Vector of Sequential Powers of 10
To create the array {1; 10; 100; 1000; ... 10^(n-1)} use
{ =10^(ROW(OFFSET(INDIRECT("A1"),0,0,n,1))-1) } -or- { =10^(ROW(INDIRECT("1:"&n))-1) }
In Office 365! =10^SEQUENCE(n,,0)
Formulas for Matrices
Excel contains some key functions for working with matrices:
- MUNIT(m): Creates an Identity matrix of size m x m
- MMULT(A,B): Uses matrix multiplication to multiply an n x k matrix A by a k x m matrix B resulting in an array of size n x m.
- TRANSPOSE(A): Switches rows to columns or vice versa, and can be used for more than just numbers.
- MDETERM(A): Calculates the determinant of a matrix A.
- MINVERSE(A): Calculates the inverse of the matrix A (if possible).
- INDEX(A,n,0) or INDEX(A,0,m): Returns either row n or column m of matrix A.
NOTE Excel does a great job of displaying data, but if you need to do a lot of statistical analysis and linear algebra, other tools such as Python, R, and Matlab may be better.
Element-Wise Multiplication of 2 Matrices
You can perform element-wise multiplication of 2 matrices by simply multiplying two ranges and entering the function as an Array Formula. For example, the formula ={1,2;3,4}*{a,b;c,d} would return the array {1*a,2*b;3*c,4*d}. If one matrix has more columns or rows than the other, those values will be truncated from the result.
Creating the ONES Vector and ONES Matrix
The ones vector j={1;1;1...} and the ones matrix J={1,1;1,1} are very useful in linear algebra and array formulas. The image below shows an example using the MUNIT function to create the Identity matrix I, the ones vector j, and the ones matrix J.
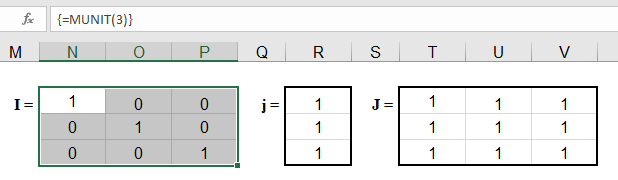
A simple way to create an n x n ones matrix (J) is to multiply the identity matrix by 0 and add 1, like this:
{ =1+0*MUNIT(n) }
The ones vector (j) of size n x 1 can be created by using INDEX to return the first column of the ones matrix, like this:
{ =INDEX(1+0*MUNIT(n),0,1) }
In older versions of Excel that don't support the MUNIT function, you can create the ones vector, ones matrix and identity matrix using these formulas:
j =(1+0*ROW(INDIRECT("1:"&n))) J =IF(ISERROR(OFFSET(INDIRECT("A1"),0,0,n,n)),1,1) I =IF( ROW(OFFSET(INDIRECT("A1"),0,0,n,n)) = COLUMN(OFFSET(INDIRECT("A1"),0,0,n,n)), 1, 0)
In Office 365! j =SEQUENCE(n,,1,0) J =SEQUENCE(n,n,1,0)
Repeating Rows or Columns to Create a Matrix
Sometimes you may need to form a matrix by repeating a row or column. This can be done using MMULT and the ones vector.
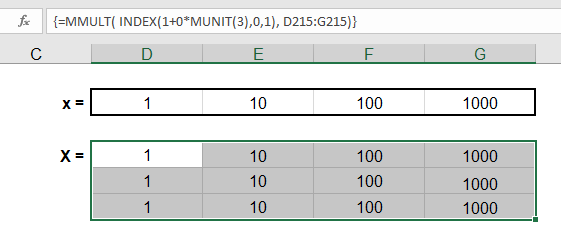
If you want to create a matrix with n rows by repeating row={1, 2, 3}, use the array formula =MMULT(j,row) where j is size n x 1.
{ =MMULT( INDEX(1+0*MUNIT(n),0,1), row) }
If you want to create a matrix with k columns by repeating col={1;2;3}, use the array formula =MMULT(col,TRANSPOSE(j)) where j is size k x 1.
{ =MMULT(col, TRANSPOSE(INDEX(1+0*MUNIT(k),0,1)) ) }
ROW or COLUMN Sums using the ONES Vector
It turns out that the ONES vector is very important in statistics for performing a very simple matrix operation: summing the rows or columns. Let's say you have a range of size n (rows) x k (columns). You could either use the SUM function separately for each row or column, or you could use array formulas.

Column-Sum: To the sum the values within each COLUMN of the matrix and return the sums as a 1 x n array (or row vector), use
ones_vector =INDEX(1+0*MUNIT(ROWS(range)),0,1) column_sum =MMULT(TRANSPOSE(ones_vector),range)
Row-Sum: To sum the values within each ROW of the matrix and return the sums as a k x 1 array (or column vector), use
ones_vector =INDEX(1+0*MUNIT(COLUMNS(range)),0,1) row_sum =MMULT(range,ones_vector)
Creating a DIAGONAL Matrix
Element-wise multiplication of matrices can be used to create a Diagonal matrix. A Diagonal matrix is a special matrix where all of the off-diagonal terms are zeros. To create the Diagonal matrix, you multiply the matrix by the Identity matrix of the same size:
Diagonal =A*MUNIT(ROWS(A))
Many programs (but not Excel) include a function like diag(matrix) which returns an n x 1 vector containing the diagonal terms of an n x n matrix. To return the diagonal as a vector, you can use the row-sum operation on the Diagonal like this:
diag(A) =MMULT(A*MUNIT(ROWS(A)),(1+0*ROW(INDIRECT("1:"&ROWS(A)))))
In Office 365! diag(A) =LET(m,A,d,SEQUENCE(ROWS(m),,1),INDEX(m,d,d))
Find the TRACE of a Square Matrix
The trace of a square matrix is just the sum of the diagonal elements. Therefore, the formula for calculating the trace is just:
trace(A) =SUM( A*MUNIT(ROWS(A)) )
Other Array Formula Examples
Linear Regression
The trend lines in an Excel chart allow you to do simple linear regression, but you can also do linear regression in Excel using matrix and array functions. It's much easier to just use the LINEST function, but for fun I give the general formula for calculating the b matrix (the least squares estimators) when you have the y and X matrix. Or in other words, if you want to solve for b starting from y=Xb, you can do that using the formula b=(X'X)-1X'y which in Excel is:
{ =MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(x),x)),TRANSPOSE(x)),y) }
Alternate XNPV Function
If for some reason you don't like Excel's XNPV function or for some reason you need to use 360 days in a year instead of 365, you can use the following array formula in place of XNPV, where r is the discount rate.
{ =SUM(values_range/((1+r)^((date_range-INDEX(date_range,1))/365))) }
Running XIRR Formula
My Investment Tracker calculates an annualized compounded rate of return using a running XIRR array formula.
Some References for Array Formulas in Excel
- Guidelines and Examples of Array Formulas at support.office.com
- Array Formulas at cpearson.com - Some detailed information about using array formulas in Excel, along with some example array functions.
- Matrix Functions in Excel at bettersolutions.com - Examples showing the use of MDETERM, MINVERSE, MMULT, and TRANSPOSE.
- Using Excel to find Eigenvalues and Eigenvectors
- A.C.Rencher, Methods of Multivariate Analysis, John Wiley & Sons, Inc.: New York, 1995.



Comments
Great stuff! Thank you for sharing.
Thank you very much, very usefull for me :)
Hi Jon:
This was a very helpful post. I have been struggling with min max in arrays for a long time and cant find any short way of doing this.
For example If i have two arrays A={2,6,2} Which translates to B={2,2+6,2+6,+2} and a Constant of C=4, and want to run the following calculation Max(Min(A,B-C),0) Resulting in Max({-2,4,2},0) = {0,4,2}.
Right now I have to do the following If(A<B-C,A,B-C). As you can imagine the conversion of A to B in itself is a long formula so repeating that long formula twice in the same formula makes it long and hard to audit. Can you please help with this?
Thanks in advance,
Akshay
@Akshay, MIN(A1:A3,B1:B3) entered as an array formula is not the same as {MIN(A1,B1),MIN(A2,B2),MIN(A3,B3)}. Instead, MIN returns a single result that is the minimum of all values within A1:A3 and B1:B3, even if you enter it as an array formula. So, I don’t think MIN(A,B-C) will work for you. Perhaps you could store the result of B-C in a separate array so that you can reference that result instead of repeating the formula that is calculating B?
Can we add the MUNIT function in the older version of excel?
@devleena, Maybe an add-in exists that adds custom functions to older versions of Excel.
I need help Max n Min array functions!
Please reply to my email so I can send the pics of my questions.
Thanks
@Eliki … See the Contact page.
Very Useful Tutorial
Thanks a lot
Thanks so much! It’s very helpful!
Does anyone know a function / formula that will enable me to add individual row values to each individual column value to create a table of the sums? I have 50 rows and 50 columns that i need the sum for each combination.
any help would be appreciated
Use $ signs to prevent a column letter or row number from changing when you copy a cell. If you have numbers in column A that need to be added to Row 1, then B2=$A2+B$1, then copy that over and down. Google “Relative vs. Absolute References in Excel” to look for more help.
Jon,
Thanks, this works perfectly! I appreciate the help.
If “A” is your column of 50 numbers in column {A1:A50} and “B” is your row of 50 numbers in {B2:AY1}, you can calculate the sum of the individual cells A1+B1 ; A2+C1 ; A3+D4 ; ……. ; A50+ AY1 by the expression C = A + TRANSPOSE{B}.
This gives a column of 50 numbers .
If you want the result displayed in a row use C = B + TRANSPOSE{A}.
“To select all the cells within a multi-cell array: Press F5 > Special > Current Array.”
Thank you – I’ve been looking for a trick for this for ages!
Or you could just use SUMPRODUCT for the first example. No array needed.
Yes, but the point of the article is to explain array formulas (starting with simple examples), not specifically the most efficient or easy way to do that particular example.
It took me many hours to figure this out: You have to SELECT the cells to which you want to expand the array before using Ctrl + Enter + Shift.
Is there a way to avoid having to do this? I would much rather just select a single cell and have the array auto-expand to the proper cells.
I’m grateful for how your soft copy has enlightened me on array formulas.God bless you alot
Date Product ID Previous Stock Quantity In Quantity Out Current Stock
01-06-23 Product A 50 10 5 55
01-06-23 Product B 50 5 10 45
01-06-23 Product C 50 10 5 55
02-06-23 Product A if the b5 is product a, the answer will be f2 (55) to be received. Its via after matching of the b2 (Prodcut A) which against the result found of above date as the last entry in the ‘B’ Column 20 12 63
02-06-23 Product B 45 10 5 50
02-06-23 Product C 55 15 10 60
03-06-23 Product A 63 15 10 71
03-06-23 Product B 50 15 10 55
03-06-23 Product C 60 15 10 65
Hi, great article!
However, I did find a minor mistake in the steps of the section:
“A Simple Array Formula Example”
Step 2: =SUM( {10*0.5;5*0.2;8*0.7;3*0.5;12*0.09} )
should be:
Step 2: =SUM( {10*0.5;5*0.2;8*0.07;3*0.5;12*0.09} )
The following step is correct, though:
Step 3: =SUM( {5;1;0.56;1.5;1.08} )